In such cases where the events are mutually exclusive and collectively exhaustive, it is preferable to use tree diagram to find the final outcome. The tree diagram for the given problem is as shown:
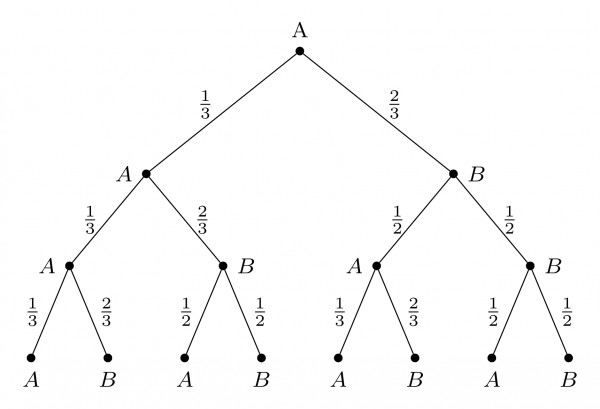
The frog is at $B$ at $t = 3$
$\implies P(A .A.B ) + P(A.B.B) + P(B.A.B) + P(B.B.B)$
$=\frac{1}{3}\times \frac{1}{3}\times \frac{2}{3} + \frac{1}{3}\times \frac{2}{3}\times \frac{1}{2} + \frac{2}{3}\times \frac{1}{2}\times \frac{2}{3} + \frac{2}{3}\times \frac{1}{2}\times \frac{1}{2}$
$=\frac{2}{27} + \frac{1}{9} + \frac{2}{9} + \frac{1}{6} = \frac{31}{54}$
Hence we have $P($frog is at $B$ at $t = 3) = 31/54$
Correct Answer: $B$