Binary search tree will be$:$
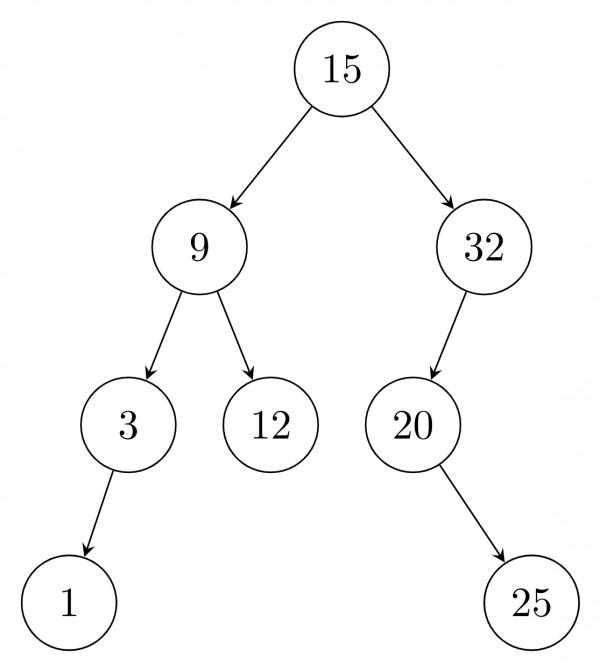
After delete of root: use inorder predecessor
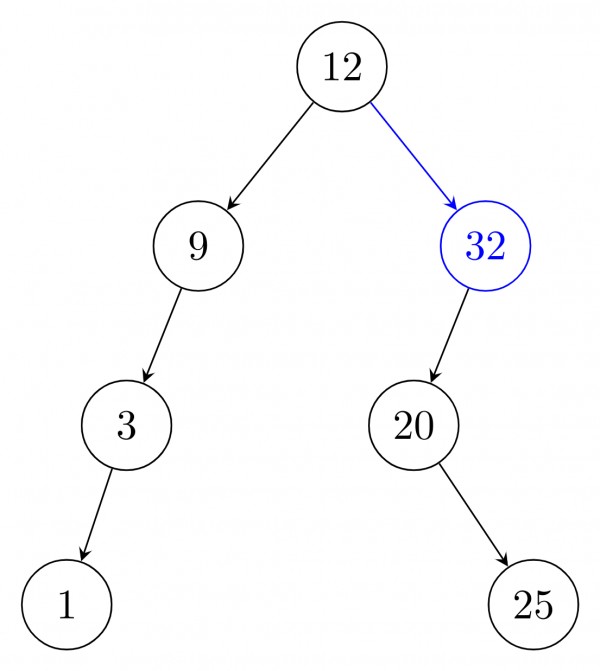
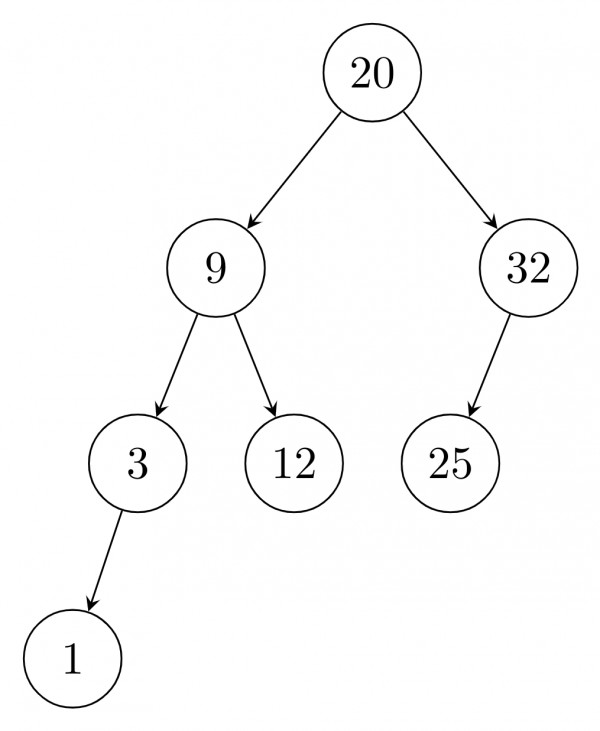
Or After delete of root: use inorder successor
typedef struct tnode{
int key;
struct tnode *left, *right;
} *Tree;
int depth (Tree t)
{
int x, y;
if (t == NULL) return 0;
x = depth (t -> left);
S1: y = depth (t -> right);
S2: if (x > y) return (1+x);one for root
S3: else return (1+y); one for root
}