[ need @arjun Sir to verify this contents ]
Collision Vector CV = $C_{m}C_{m-1} \cdots C_{3}C_{2}C_{1}$ Where
if $C_{i} = 0 \Rightarrow$ Permissible Latency
if $C_{i} = 1 \Rightarrow$ Forbidden Latency
Given CV : 1011010
Permissible Latency = 1,3,6
Forbidden Latency = 2,4,5,7
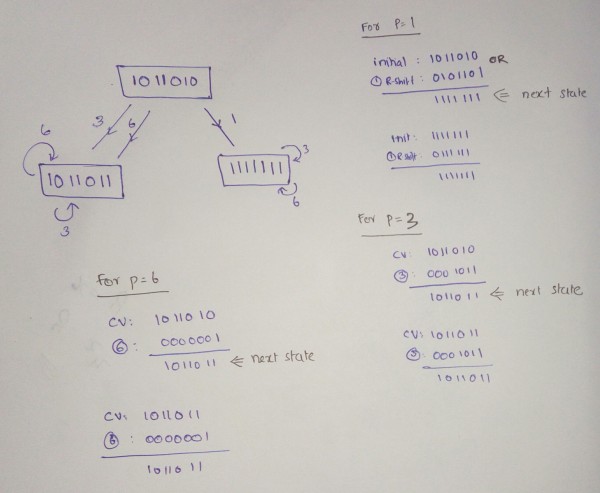
Step 1 : Constructing State Diagram
How to draw the state diagram ?
Initial State : 1011010
Step 1.a : Right Shift Inital State with 'p' - permissible latency times
For p=1
Right Shift '1' time intical CV : 1011010 $\Rightarrow$ 0101101 .
Step 1.b : Perform OR operation with Initial CV with Right Shifted Value
Initial CV $\Rightarrow$ 1011010 OR
'1' R-shift$\Rightarrow$ 0101101
______________________________________
Next State$\Rightarrow$ 1111111
Step 1.c : Perform step 1.a and step 1.b As many times untill same state repeats
New CV : 1111111
Step 1.a
Right Shift '1' Time : 0111111
Step1.b
1111111 OR 0111111 $\Rightarrow$ 1111111
FOR p=3
Initial State : 1011010 OR '3' R-shift 0001011 $\Rightarrow$ 1011011 ( next state)
Initial State : 1011011 OR '3' R-shift 0001011 $\Rightarrow$101011 ( state Repeating )
For p=6
Initial State : 1011010 OR '6' R-shift 0000001 $\Rightarrow$ 1011011 ( next state)
Initial State : 1011011 OR '6' R-shift 0000001 $\Rightarrow$101011 ( state Repeating )
This proceure can be simplified in the following diagram .
When Number of Shifts is 'm+1' or grater all transitions are returned back to inital state we denote this as (m+1)+ Here m=7 , Therfore 8+
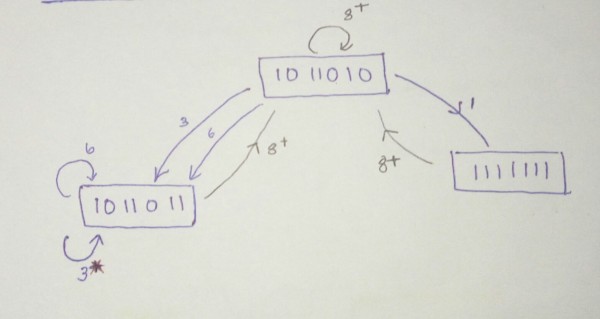
Step 2 : Determining MAL
Step 2.a : Find the number Of Simple Cycle
Formally
" Simple Cycle are those latency cycles in which each state appears only once per each iteration of the cycle "
Informally
There should be a cycle and each state should be visited exactly once
Here 3,6,8, (1,8) , (3,8) , (6,8) are simple cycles
Step 2.b : Find the Greedy Cycles
Formally
A single cycle is a greedy cycle if each latency contained in the cycle is the minimal latency (outgoing arc) from a state in the cycle.
Procedure to determine the greedy cycles
1. From each of the state diagram, one chooses the arc with the smallest latency label unit; a closed simple cycle can formed.
2. The average latency of any greedy cycle is no greater than the number of latencies in the forbidden set, which equals the number of 1’s in the initial collision vector.
3. The average latency of any greedy cycle is always lower-bounded by the MAL in the collision vector
Informally
$\triangleright$ Edges are made with min Latency
$\triangleright$ Average Latency is lower than other simple cycles
Here , Among all the Simple cycles Avg latency is minimum for
cycle 3, (1,8)
$\frac{1+8}{2} = 4.5$
Step 2.c : Determining MAL
MAL is the minimum of the avegrage latency cycles ,
Here it is 3
MAL is 3
MAL edges are marked with *
Source : Advanced Computer Architecture , KAI HWANG
Good Read : GATE 2015 SET 3 Question on MAL