Lets draw the truth table for $P$ ∨ $Q$ along with $P \ □ \ Q :$
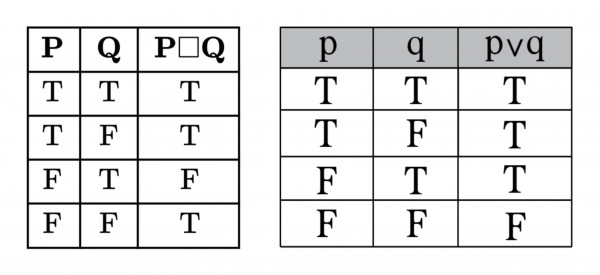
If we observe the truth table, $P$ ∨ $Q$ and $P \ □ \ Q $ is differ in only last two cases.
So if we replace $Q’$ in place of $Q$ in $P$ ∨ $Q$ truth table, it will be like $:$
| P |
Q |
P V Q’ |
| T |
T |
T |
| T |
F |
T |
| F |
T |
F |
| F |
F |
T |
This is exactly same truth table as of $P \ □ \ Q $
So, from here we can conclude $:$
$P$ ∨ $Q’$ $=$ $P \ □ \ Q $
==> $P$ ∨ $(Q’)’$ $=$ $P \ □ \ Q’ $ [Replacing Q by Q’ in both side]
==> $P$ ∨ $Q$ $=$ $P \ □ \ Q’ $
$Correct \ Ans \ : Option \ B$