This is also based upon the cut property of the spanning trees.
For the property, I refer you to theorem 23.1 of Cormen 3rd edition.
Consider I have below scenario where I have two components, X and Y and vertex s lies in X and vertex t lies in Y.
I have recursively further divided the component of X into two more components X1 and X2 having vertex A and B respectively.
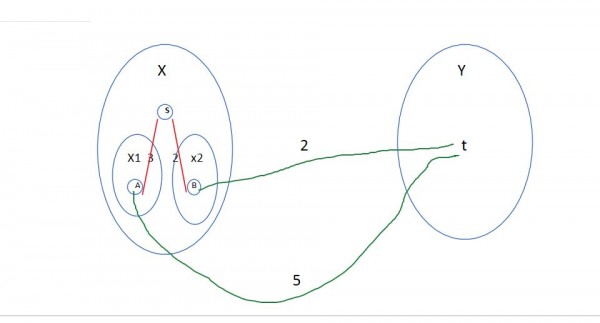
Consider congestion of edge S-A=3,S-B=2, A-T=5 and B-T=2.
At every step, I choose light edge (minimum weight edge which joins two distinct components of the graph)
So, first I select edge S-B. Then I select edge B-T and this path to T from S via B is of minimum congestion. And this is nothing but how your spanning tree algorithm works.
Answer-(A)