Given program:
#include <stdio.h>
double foo(int n) {
int i;
double sum;
if(n == 0) {
return 1.0;
}
else {
sum = 0.0;
for(i = 0; i < n; i++) {
sum += foo(i);
}
return sum;
}
}
int main() {
double a = foo(5);
printf("%.2f\n",a);
}
And here is the present situation :
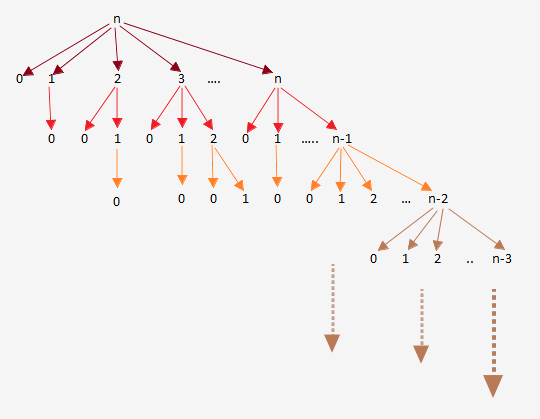
Here we can see that, we have lots of overlapping subproblems. Too many function calls.
- No of function calls = $2^n$
- stack depth used = $O(n)$
Therefore space is linear and time is exponential.
If we take a small number say $4$, then we would have $8.0$ as answer, or we can see that $foo(n) = 2^{n-1}$
and
- stack depth used = $5$.
- No of function calls = $2^4 = 16$.

Now, using one-dimensional ($1D$) table we can reduce the no of function calls and depth of stack space used as well.
Here is what we want to achieve:
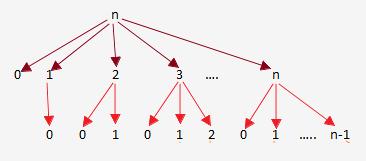
We are reusing already computed $foo(x)$ values. For this purpose, we will be using one $1D$ array of doubles of size $n$.
Here is what we are going to do:
- First, check in the $1D$ table for the required call value.
- If correct value found: do not call recursive functions
- If not, then only attempt
for loop recursive calls
Here is the code:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#define UNUSED 0.5
double *memo_table;
double foo(int n) {
int i;
double sum;
if(memo_table[n] != UNUSED) {
return memo_table[n];
}else {
sum = 0.0;
for(i=0;i<n;i++) {
sum += foo(i);
}
return memo_table[n] = sum;
}
}
int main() {
int n,i;
scanf("%d",&n);
memo_table = malloc((1+n)*sizeof(double));
for(i=0;i<=n;i++) memo_table[i] = UNUSED;
// base case
memo_table[0] = 1.0;
double a = foo(n);
printf("%lf\n",a);
free(memo_table);
}
Improvements over given program:
- Stack space because of function calls reduced to two level only.
- Extra space used for the $1D$ array = $O(n)$
- More importantly, Time is reduced to $O(n^2)$. (Exponential to Quadratic !! )
Overall space complexity = stack + extra = $O(1) + O(n) = O(n) $
Answer is B.