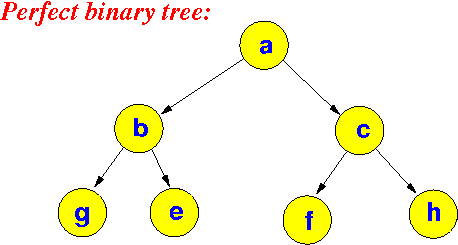
Number of nodes is maximum for a perfect binary tree. A binary tree of height h has 2
$2^{h+1} - 1$ nodes.
$2^{5 + 1} - 1 = 2^{6} - 1 = 63$
Number of nodes is minimum for a skewed binary tree. A binary tree of height h has h+1 nodes.
$h + 1 = 5 + 1 = 6$
