GATE2015-2-45

Question

Suppose you are provided with the following function declaration in the C programming language.

int partition(int a[], int n);

The function treats the first element of $a[\:]$ as a pivot and rearranges the array so that all elements less than or equal to the pivot is in the left part of the array, and all elements greater than the pivot is in the right part. In addition, it moves the pivot so that the pivot is the last element of the left part. The return value is the number of elements in the left part.

The following partially given function in the C programming language is used to find the $k^{th}$ smallest element in an array $a[\:]$ of size $n$ using the partition function. We assume $k \leq n$.

int kth_smallest (int a[], int n, int k)
{
    int left_end = partition (a, n);
    if (left_end+1==k) {
        return a[left_end];
    }
    if (left_end+1 > k) {
        return kth_smallest (___________);
    } else {
        return kth_smallest (___________);   
    }
}

The missing arguments lists are respectively

• A. $(a,$ left_end$, k) $ and $ (a+$left_end$+1, n-$left_end$-1, k-$left_end$-1)$
• B. $(a,$ left_end$, k) $ and $ (a, n-$left_end$-1, k-$left_end$-1)$
• C. $(a+$ left_end$+1, n-$left_end$-1, k-$left_end$-1) $ and $(a, $ left_end$, k)$
• D. $(a, n-$left_end$-1, k-$left_end$-1)$ and $(a, $left_end$, k)$

Comments

Option C is wrongly typed here. Please correct it. It is (a + left_end+1, n-left_end-1, k-left_end-1)

---

We can direct eliminate the options b,c, and d because in the second condition when  left_end+1 < k 
base address of the array (a) will not be passed in the function call.

---

@ Manu Thakur May you please explain a lit bit more in a naive way!

---

can you explain it a bit?

---

It's because, when left_end+1 < k  it means the kth element will be found in the RHS sub part, So we will leave the first half part and apply the procedure on the second half only, a represents the base address, hence a will not be provided as the address of array. hence we can eliminate the options b,c and d.

There is one point worth noting here is that left_end is the count of numbers less than pivot element, including pivot the count is left_end+1.

---

All of the options are hideously misprinted.

---

Thanks for the explanation @chauhansunil20th

Answer 1

We have to find the $k^{th}$ smallest element.

if (left_end+1 > k) 

If the above condition is true, it means we have $k^{th}$ smallest element on the left array, whose size is left_end instead of $n$ for the original array. (The "+1" is used because array index in C language starts from 0). So, we can do a recursive call as 

• kth_smallest( a, left_end, k); 

If the above condition is false, and left_end $+1\neq k,$ it means $k^{th}$ smallest element is on the right part of the array and it will be $(k - \text{left_end}-1)^{th}$ element there as left_end+1 elements are gone in the left part. So, the recursive call will be 

• kth_smallest( a + left_end + 1, n - left_end_1, k - left_end - 1); 

Correct Option: A.

Comments

Plz explain more.

It works for unsorted array too. right??

Then what is the funda of finding unsorted array and kth element at the same time?

---

The behavior of partition function is that it will take the pivot element to it's sorted place(As all the smaller elements are in the left side and greater or equal elements are in the right side. Making the pivot the peak element)

Assuming the array: 33, 64, 3,  3, 4, 34 ,11,66

Now taking the pivot as 33(The first index)

The result will look like : (3,3,4,11 smaller elements) ,33, (64,34,66 greater elements)

Now the 33 is at it's correct position(Just as it would have been in an sorted array) in the array.This partition behavior can the of the use in finding kth smallest element.

Let k be 7 for the above example.

The return value is (left_end=4) by the partition function. Which is smaller than k so we will search the upper half of the array (a+left_end+1)(The base index is now pivot+1 element's index) and making the value of n as the size of the upper array and the value of the as k-left_end-1 because left_end and pivot belongs to the left array and the new k value will be according to the right array.

new values are

Array: 64,34,66

n = 3, k = 2

Applying partition again 34,(64),66 it will return the left_end = 1 and left_end+1 = 2 = K which is our element.

---

got it , it's too confusing when you try it in first go.

---

The return value must be left_end=5 right because it is mentioned in question that pivot is also included in left part and return value must 4+pivot(1) =5 ?

---

Yes!

---

But if we take like that we get wrong value?

Answer 2

First of all, here the return value is the number of elements less than the pivot

Pivot is just to minimize searching

So, now we are assuming our array has $10$ elements, $N=10 , k=8$

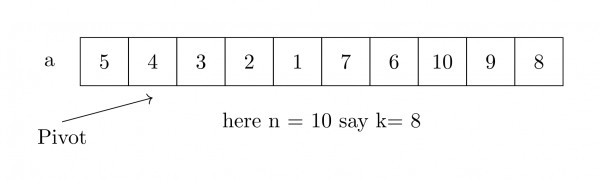
STEP 1:          After Partition()

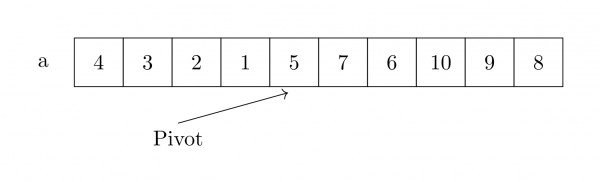
• left_end = 4
• left_end+1 < k
• so, (a+left_end+1, n-left_end-1, k-left_end-1)
• (a+5, 5, 3)

STEP 2: After  Partition()

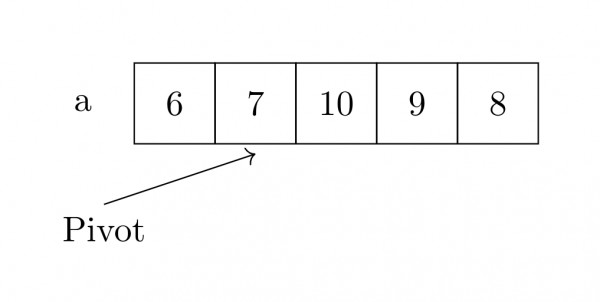
• left_end= 1
• left_end+1 < k
• so, (a+2, 3, 1)

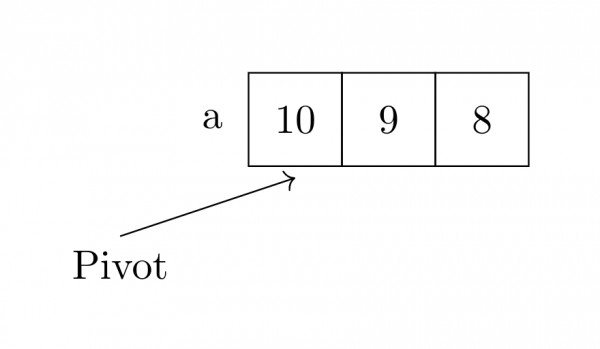
STEP 3: After Partition()

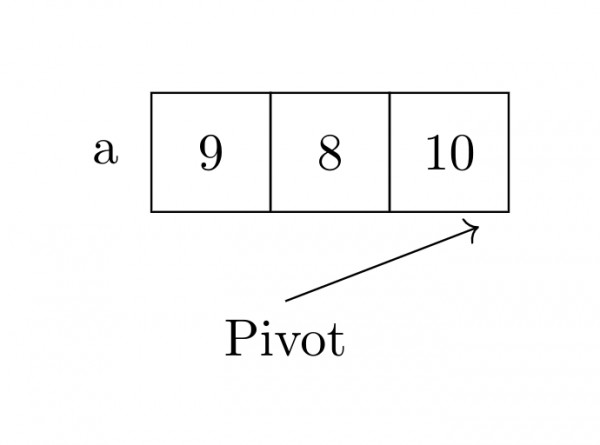
• left_end = 2
• left_end +1 > k
• so, (a, 2, 1)

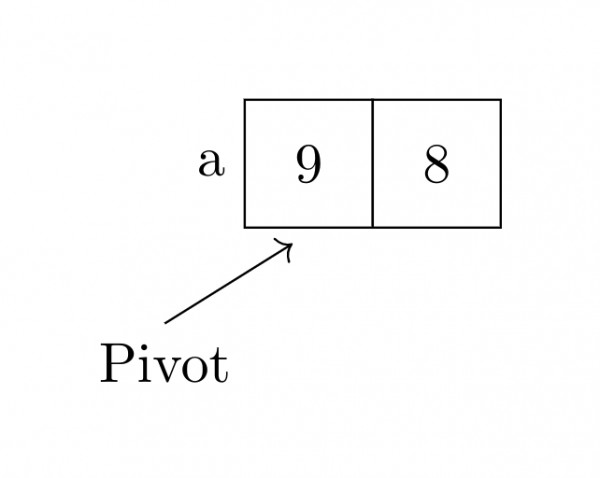
STEP 4: After Partition()

• left_end = 1
• left_end +1 > k
• so, (a,1,1)

STEP 5:

• left_end = 0
• left_end+1 = =k
• a[left_end] = 8

So, in STEP 1 and STEP 2 'else' condition is satisfied, and STEP 3 and STEP 4 'if ' condition is satisfied.

Here, partition is called and it returns the left_end value

Answer will be (A).

Comments

u can prove the left part with this . but u will miss the right condition. as there are options for right part also . i think u should have take a normal array . or just follow the first answer. if the kth smalles is not found then it will be on the left side . else on right . make condition leaving the left end . so on left -1 and on right +1 hence option a .

---

@Tendua

I am not getting u

I have taken a normal array only

and after calling partition() on that array I got this array i.e. showing in picture.

It I have mentioned in the 1st line of my answer

right?

---

if u know about the worst case of the quick sort . sorted array is the worst case ( increasing or decreasing ) and partition just place only one object in it place not sort the whole array. read question once again .

---

"all elements less than or equal to the pivot is in the left part of the array"

So, array should be increasing only. right?

---

Now, see the ans @Tendua

---

@Srestha After step 1 your array shouldn't be 1 4 3 2 5 7 6 10 9 8?

---

why that will be?

---

because in quick sort pivot element is replaced with ith element

---

@ srestha ma'am, left_end always returns number of elements in left part of the array including pivot as mentioned in the line 

all elements less than or equal to the pivot is in the left part of the array, and all elements greater than the pivot is in the right part. 

so shouldn't after 1st step, left_end=5 ??  

Thats how its different from normal partition method where we generally keep (left) pivot (right) i.e fixing pivot as it gets to its correct position in the array. But this question seems to have a modified definition of partition function.

---

@SRESHTA i also have same doubt as of meghna

---

On step 3 when u took 10 as pivot

Then u chk from last element 8 which was less than 10 so dec j and i will remain same

Then chk 9 which is also less so dec j and i will again remain same

Then we reach pivot(10) so Dec i which is at 8 and swap 8 and 10

And the array will become 8 9 10

How does the array become 9 8 10

---

why return value does not include pivot as it should no of element in left including pivot. @srestha mam?

---

@srestha You have said that return value is no. of element less than pivot but question says that return value is no. of element in left part and pivot is the last element of left part.pls clerify

---

@prabhas44

I havenot got u. Is there anything, while executing the program?? Where exactly r u getting problem?

---

I think , pivot definition is here like this "all elements less than or equal to the pivot is in the left part of the array,"

---

I stucked at "Left_part+1=k" wala condition. I think it should be Only "Left_part=k ".Any way i got the ans by elimination method.Thanks For Reply

---

@prabhas44

Can u plz. tell me, how r u doing option elimination??

Answer 3

Ans A.

Comments

Although [option A] is correct answer, but sometimes the wording in the question creates problem.

Lines from the Question:
"it moves the pivot so that the pivot is the last element of the left part. The return value is the number of elements in the left part."
If the underlined words means that the pivot belongs to left part, then the number of elements in the left part includes the pivot and therefore there is an infinite recursion for a particular instance.

Particular Instance:   a = {5, 1, 2, 3, 4, 6, 7, 8, 9, 10}, n = 10, k = 5

Call 1:
Before partition :  a = {5, 1, 2, 3, 4, 6, 7, 8, 9, 10}, n = 10, k = 5
partition(a, 10); pivot = a[0] = 5
After partition  :  a = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
LeftPart = {1, 2, 3, 4, 5}  <-- pivot 5 belongs to LeftPart
left_end = 5 = number of elements in LeftPart

Call 2:  (left_end+1 > k) = (5+1 > 5) = true
Before partition : a = {1, 2, 3, 4, 5}, n = 5, k = 5
partition(a, 5); pivot = a[0] = 1
After partition  : a = {1, 2, 3, 4, 5}
LeftPart = {1}  <-- pivot 1 belongs to LeftPart
left_end = 1 = number of elements in LeftPart

Call 3: (left_end+1 > k) = (1+1 > 5) = false
Before partition : a = {3, 4, 5}, n = 3, k = 3
partition(a, 3); pivot = a[0] = 3
After partition  : a = {3, 4, 5}
LeftPart = {3}  <-- pivot 3 belongs to LeftPart
left_end = 1 = number of elements in LeftPart

Call 4: (left_end+1 > k) = (1+1 > 3) = false
Before partition : a = {5}, n = 1, k = 1
partition(a, 1); pivot = a[0] = 5
After partition  : a = {5}
LeftPart = {5}  <-- pivot 5 belongs to LeftPart
left_end = 1 = number of elements in LeftPart

Call 5: (left_end+1 > k) = (1+1 > 1) = true
Before partition : a = {5}, n = 1, k = 1
partition(a, 1); pivot = a[0] = 5
After partition  : a = {5}
LeftPart = {5}  <-- pivot 5 belongs to LeftPart
left_end = 1 = number of elements in LeftPart

Call 6: (left_end+1 > k) = (1+1 > 1) = true
Before partition : a = {5}, n = 1, k = 1
partition(a, 1); pivot = a[0] = 5
After partition  : a = {5}
LeftPart = {5}  <-- pivot 5 belongs to LeftPart
left_end = 1 = number of elements in LeftPart

....
Call 5 is same as Call 6, and this goes into infinite recursion.
....

---

When n = 1, the code goes to infinite recursion rt?

The return value is the number of elements in the left part

This should have been

The return value is the number of elements less than the pivot

---

Yes. Or it should have been

"it moves the pivot so that the pivot is next to the last element of the left part.

---

how does the partition algorithm works when first element is pivot?how is the algorithm changed when pivot is last element?

---

yes,this is confusing that whether it returns number of elements on left part including pivot or not?

But if we look at code's first statement ,it means that it returns number of elements on left excluding pivot

---

in first go I'm also include the pivot element in left part, it's very ambiguous that we have to include the pivot or not. But if we think deeply they mentioned    "it moves the pivot so that the pivot is the last element of the left part. The return value is the number of elements in the left part." 

this mean they said we have to include it that's why we got infinite recursion for some sequence.

Answer 4

Dry run it.

If the "if" condition is true, required element is in the left part of the array. So, we need to pass just the left part of the array, as the whole array.

If the "else" condition is true, required element is in the right part of the array. So, we need to pass just the right part of the array, as the whole array.

So, option A

 

Also, adding from Manu Thakur's comment — in the else part, we need to recursively call just the right part of the array as the complete array. It obviously won't always start with the base address (a), hence Options B, C and D are directly eliminated.