GATE CSE 2015 Set 3 | Question: 5

Question

The number of $4$ digit numbers having their digits in non-decreasing order (from left to right) constructed by using the digits belonging to the set $\{1, 2, 3\}$ is ________.

Comments

@Kanwae Kan This formulae will work for non-decreasing order and non-increasing order . This will not work for increasing and decreasing order.

You can cross check with small set of elements.

---

@Deepak Poonia Sir how will we solve this type of questions if size of set of elements is large. because then brute force will be time consuming!!

---

@abir_banerjee

This question is based on IODB template(Star Bars Problem) of Objects distribution into Boxes. Even if size of set of elements is large, the question is Easily & efficiently solvable.

Watch this lecture: https://youtu.be/0oRBHg1ERtU 

Answer 1

We can arrive at a solution by constructing a graph for each starting digit. For example root $3$ means - starting with $3$ it can have $3$ children $1,2,3$ and the construction goes.

$3$ can have three children $1, 2,3$

$2$ can have two children $1, 2$

$1$ can have only $1$ as child.

Graph need to be done till four levels as we need $4$ digits and we have $3$ such graphs starting with $3$, $2$ and $1.$
And finally count the total number of leaves of all the graphs gives our answer as $15.$

Comments

JUST WOW!!

---

oooooppp….finally  best answer thanks

---

Can we always apply this approach in this variety of questions like decreasing ,increasing ?

Answer 2

Dynamic Programming Approach

$$\begin{array}{|c|c|c|c|c|} \hline \textbf{} &  \textbf{1 digit}& \textbf{2 digits} & \textbf{3 digits} & \textbf{4 digits} \\\hline \textbf{Starting 3} & 1 & 1 & 1 & 1  \\\hline \textbf{Starting 2} & 1 & 2 & 3 & 4 \\\hline \textbf{Starting 1} & 1 & 3 & 6 & 10 \\\hline \end{array}$$

Here Starting $1$ means numbers starting with $1$. And cell $(i, j)$ is for number of numbers starting with $i$ and having $j$ digits. We can have the relation $$ c(i, j) = \Sigma_{k=1}^i c(k, j-1)$$ as per the non-decreasing condition given in the question. So, our answer will be $$c(1,4) + c(2, 4) + c(3, 4) = 1 + 4 + 10 = 15$$

---

Brute force

• 3 3 3 3
• 2 2 2 2
• 2 2 2 3 
• 2 2 3 3
• 2 3 3 3
• 1 1 1 1
• 1 1 1 2
• 1 1 1 3
• 1 1 2 2
• 1 1 2 3
• 1 1 3 3
• 1 2 2 2
• 1 2 2 3
• 1 2 3 3
• 1 3 3 3

Comments

great explanation @Arjun sir

---

@Rishab I used the same method and is correct because it is equivalent of finding monotically increasing or decreasing functions.

---

Dynamic Programming Approach

Let $n$ = total no. of elements in the set where the elements are in ascending order.

$c(i,j)$ denote the possible no. of numbers of $j$ digits such that the $j^{th}$ digit (from right) is the $i^{th}$ element of the set. 

The recurrence relation is as follows-

$c(i, j) = 1, \ j=1$

$c(i, j) = \sum_{k = i}^{n} c(k, j-1) \ \forall \ j>1$

Example

Given, set is $\left \{ 1, 2, 3 \right \}$.

Here, $n = 3$.

Therefore, $c(2,3) = \sum_{k = 2}^{3} c(k, 2) = c(2,2) + c(3,2) = 3$

The resultant table will be as follows-

	1 digit	2 digit	3 digit	4 digit
$1^{st}$ element (1)	1	3	6	10
$2^{nd}$ element (2)	1	2	3	4
$3^{rd}$ element (3)	1	1	1	1

NOTE: Cells are filled column wise.

Finally, the given question is asking about finding all such the different possible 4 digit no. that can be formed. This can be obtained by adding the values in the last column, i.e. $c(1,4) + c(2,4) + c(3,4) = 15$

Therefore, required solution is 15.

Answer 3

We can form a 4 digit number by selecting $x_1$ 1s, $x_2$ 2s and $x_3$ 3s. Then $x_1 + x_2 + x_3 = 4$. The number of solutions of this equation is $\binom{6}{2} = 15$. Each such solution can be arranged in non-decreasing order. Hence the answer is 15.

Comments

Please anybody can help ,how in this solution arrangement of numbers in  non-decreasing order been taken care ?

Thanks in advance

---

For any given combination of 4 digits, we always have exactly one non-decreasing number. eg.: 2,3,2,1 has only one combination of non-decreasing number i.e1223. So, our problem comes down to simply finding "total number of combinations where 4 digits must be selected from a set of 3 digits (1,2,3) where each digit can be repeated". For each combination, we have exactly one non-decreasing number.

---

thanks a lot ...that helped me :)

Answer 4

In such question where at each step choices get ruled out and set is small better to use tree method.

The four digit number is $d_1d_2d_3d_4$ and we start by making a tree rooted by $d_4$. This number can be any of the number from {1,2,3}.

Then, based on $d_4$ we construct the next level of tree what next nodes can it connect to so that we won't break the property of the digits such that they are non-decreasing. Have a look at trees.

The tree is not built fully for the cases where we break the non-decreasing property like in above tree when $d_3$ is 2 or 3 we didn't continue to build that tree. So, we won't count those cases.

 

 

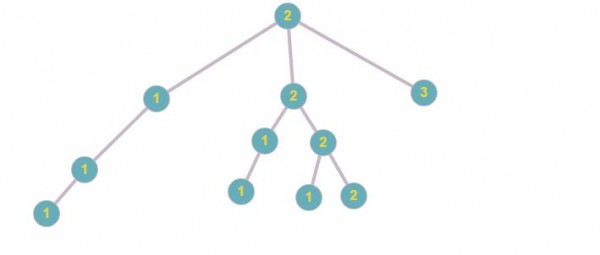
Finally in all three trees count the number of leaf nodes which are at a height of 3 and thus our 4 digited number maintaining the non-decreasing property.

so total such  numbers are 1+4+10=15

Comments

nice trick!!

---

In such question where at each step choices get ruled out and set is small better to use tree method.

Useful intuition! Thank you, sir ^_^