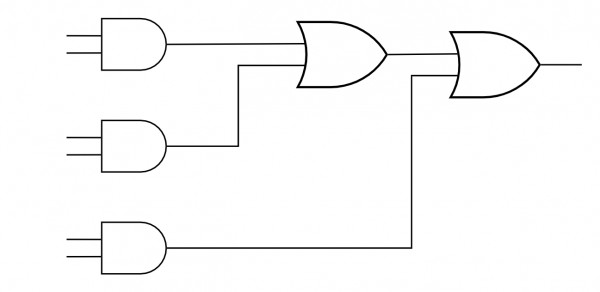
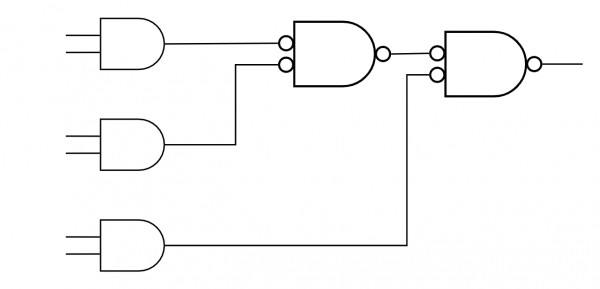
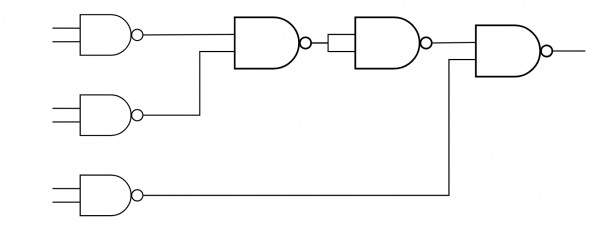
$f(x,y,z)=xy'+yz' =xy'z'+xy'z+x'yz'+xyz'$
$f(x,y,z)=\sum_m(2,4,5,6)$
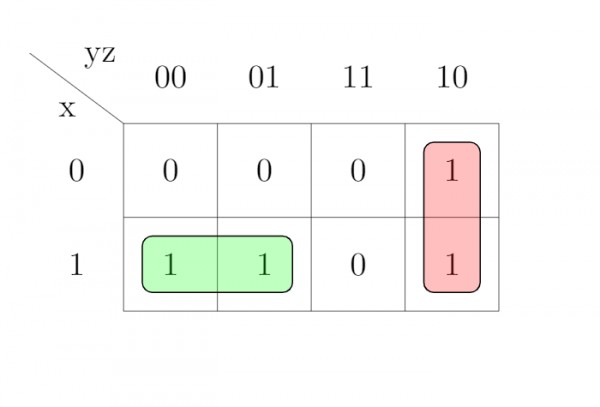 K-map
K-map
By pairing of $1's$, we get two pairs $(2,6),(4,5)$ resulting in same expression $F= xy'+yz'$
But by pairing of $0's$, we get two pairs $(0,1),(2,7)$, we get $F'= yz+x'y'$
Take complement, $F= \overline{(yz)}.(x+y)$
so we can implement the function with $1$ NOT , $1$ OR and $2$ AND gates.
For the second part , we need to implement given circuit using NANDs only.
so best way is to replace OR with Invert NAND, $A+B = \overline{(\bar A\bar B)}$