GATE1990-13a

Question

Consider the height-balanced tree $T_{t}$ with values stored at only the leaf nodes, shown in Fig.4.

(i) Show how to merge to the tree, $T_{1}$ elements from tree $T_{2}$ shown in Fig.5 using node D of tree $T_{1}$.

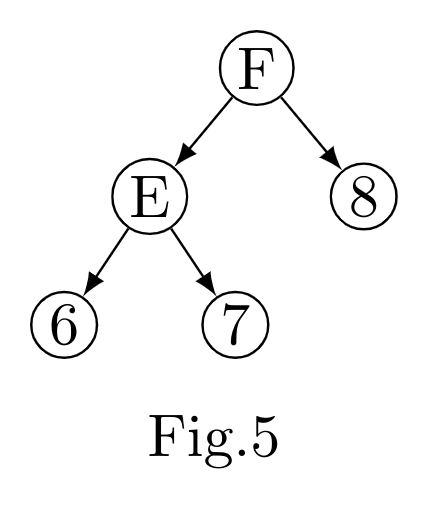
(ii) What is the time complexity of a merge operation of balanced trees $T_{1}$ and $T_{2}$ where $T_{1}$ and $T_{2}$ are of height $h_{1}$ and $h_{2}$ respectively, assuming that rotation schemes are given. Give reasons.

Answer 1

A height balanced tree is a binary tree in which the difference between the left subtree and right subtree is not greater than 1.

Since the values are stored only at the leaf nodes and the merging is done using node D, we add extra nodes as shown below  :-

Complexity will be $O(n \log n)$

As here all nodes of second tree need to be inserted in tree and rotation of nodes are needed.

Comments

How did you merge t1 and t2.. I m not getting it.. Can't we just put all elements and from t1 and t2 and perform insertion with rotation..

---

like BST

F can be right child of B and 5 will be in left subtree leaf of F

---

@srestha , I think, you have added some extra nodes..here T₁ contains 9 nodes and T₂ contains 5 nodes. So, after merging , total nodes should be 14..but in your 1^st image , no. of nodes = 15 and in 3^rd image , no. of nodes = 16...

could you please explain why time complexity is O(nlogn).. I think here we should have to write time complexity in terms of h₁ and h₂. and could you please explain what is meaning of merge using node D.

---

@ankit

I havenot added 1 extra node, I added 2 extra node

See in 1st pic after E I added 1 extra node, otherwise 5 couldnot be there in resultant tree

and yes again I added 1 extra node in 3rd pic

Because  it holds 6,7 as leaf

Basically according to question, we need to accommodate 8 nodes as leaf

---

@srestha , instead of adding one extra node , can't we add 6 to the  left of E and 5 to the left of 6 ?

---

then 6 will not be leaf

---

@srestha , is it necessary that all given leaf nodes should also be leaf nodes in the merged tree ?  it is not mentioned in the question..

---

yes, required

As this is pattern given in question

some visualization required to ans some ques

---

@srestha In First Image Left Child of E is 4 and Right Child of C is 4 can u explain please?

---

how Complexity will be O(n log n) ??

---

@mohan123 check this out

https://www.geeksforgeeks.org/merge-two-balanced-binary-search-trees/

---

O(n) tc if the use of extra space is permitted

---

yes @Bhupendra 

---

@adarsh_1997 why we did rotation on node B when D is also not balanced in 3rd Picture?

Answer 2

Superscript near the nodes indicate their Balance factor. LL and RR rotations are same as those done on AVL trees.

 

Comments

Your answer makes some sense. 🖕

@ankitgupta.1729

Brother, can you check it?