The following algorithm (written in pseudo-pascal) work on an undirected graph $G$
program Explore (G)
procedure Visit (u)
begin
if Adj (u) is not empty
{comment:Adj (u) is the list of edges incident to u}
then
begin
Select an edge from Adj (u);
Let edge be e=(u, v)
remove e from Adj (u) and Adj (v);
Visit (v);
end
else
mark u as a finished vertex and remove u from LIST
{Comment: LIST is the set of vertices in the graph}
end;
begin
While LIST is not empty
do
begin
Let v ∊ LIST;
Visit (v);
end
end.
Note: Initially $Adj(u)$ is the list of all edges incident to $u$ and LIST is the set of all vertices in the graph. They are globally accessible.
- What kind of subgraphs are obtained when this algorithm traverses the graphs $G_{1}$ and $G_{2}$ shown in Fig$.(6)$ and Fig$.(7)$ respectively?
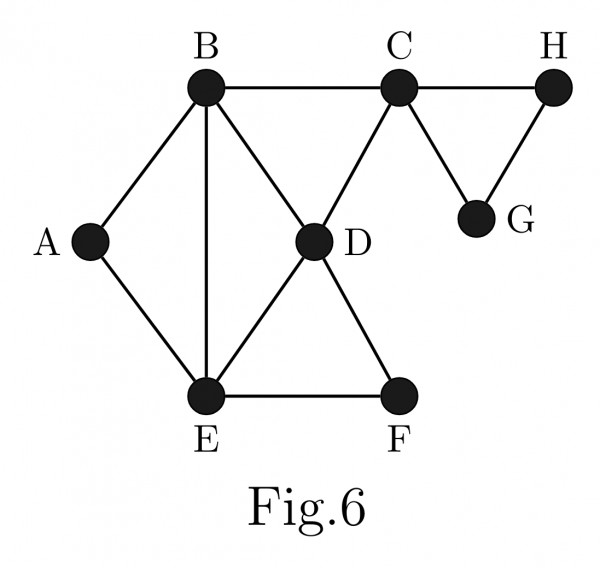

- What is the commonly Known traversal of graphs that can be obtained from the subgraphs generated by Program Explore?
- Show that the time complexity of the procedure is $O (v + e)$ for a graph with $v$ vertices and $e$ edges, given that each vertex can be accessed and removed from LIST in constant time. Also, show that all edges of the graph are traversed.