Visualizing the solution:-
Let a graph $G(6,4)$ be composed of a star graph and an isolated vertex. Here $n=6, k =2 $

MAX CASE: REMOVE THE HUB ($C$)
If we remove a vertex, all its edges must also be removed.

Now, we have $5 = n-1$ components
MIN CASE: REMOVE THE VERTEX ($F$):-
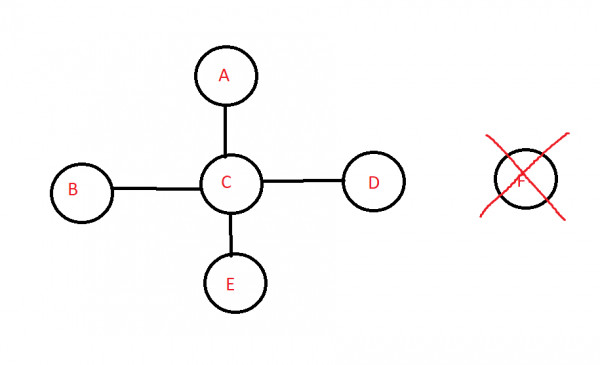
Now we have only $’1’$ = $(k-1)$ component.
Hence, by the above example, we can see that the Answer is Option (C) $k-1$ and $n-1$