- One Euivelence relation creates one partition.
- S = $\left \{ a,b,c,d,e \right \}$ ,here one possible parition is = $\left \{ \left \{ a,b \right \} , \left \{ c,d \right \} , \left \{ e \right \} \right \}$ . Tis partition has 3 groups. Corresponding EQ relation has 3 EQ classes. Note that this partition is unordered..
- So, no of different unordered partitions = No of equivalence relations.
Here the condition is we need only 3 equivalence classes. So, the partition has to be done in 3 unordered groups.
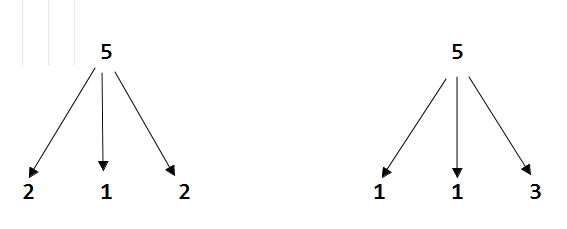
$$\begin{align*} \frac{5!}{1!1!3!}.\frac{1}{2!} + \frac{5!}{2!1!2!}.\frac{1}{2!} = 10 + 15 = 25 \\ \end{align*}$$
In case if we need maximum possible EQ relations on 5 elements.
$\begin{align*} 5 &\rightarrow 5\Rightarrow \frac{5!}{5!} = 1\\ \\ \hline \\ &\rightarrow 4 \qquad 1 \Rightarrow \frac{5!}{4!1!} = 5 \\ \\ \hline \\ &\rightarrow 3 \qquad 2 \Rightarrow \frac{5!}{3!2!} = 10 \\ \\ \hline \\ &\rightarrow 3 \qquad 1 \qquad 1 \Rightarrow \frac{5!}{3!1!1!}*\frac{1}{2!} = 10 \\ \\ \hline \\ &\rightarrow 2 \qquad 2 \qquad 1 \Rightarrow \frac{5!}{2!2!1!}*\frac{1}{2!} = 15 \\ \\ \hline \\ &\rightarrow 2 \qquad 1 \qquad 1 \qquad 1 \Rightarrow \frac{5!}{2!1!1!1!}*\frac{1}{3!} = 10 \\ \\ \hline \\ &\rightarrow 1 \qquad 1 \qquad 1 \qquad 1 \qquad 1 \Rightarrow \frac{5!}{1!1!1!1!1!}*\frac{1}{5!} = 1 \\ \\ \hline \\ &\Rightarrow \text{Total} = 1+5+10+10+15+10+1 = 52 \end{align*}$
The procedure for partitioning is , indistinguishable $\rightarrow$ indistinguishable but because of the distinct elements we need to further evaluation.
Graphically we were interested in the rectangle shown below containing 25 EQ relation or partitions.
