GATE CSE 2003 | Question: 31

Question

Let $(S, \leq)$ be a partial order with two minimal elements a and b, and a maximum element c. Let P: S \(\to\) {True, False} be a predicate defined on S. Suppose that P(a) = True, P(b) = False and P(x) \(\implies\) P(y) for all $x, y \in S$ satisfying $x \leq y$, where $\implies$ stands for logical implication. Which of the following statements CANNOT be true?

• A. P(x) = True for all x \(\in\) S such that x ≠ b
• B. P(x) = False for all x \(\in\) S such that x ≠ a and x ≠ c
• C. P(x) = False for all x \(\in\) S such that b ≤ x and x ≠ c
• D. P(x) = False for all x \(\in\) S such that a ≤ x and b ≤ x

Comments

Option D:

P(x) = False for all x ∈ S, such that a ≤ x and b ≤ x

is this right??

I think it must be a<x. Here and is written means both a≤x and b≤ x is satisfying .but if a value can be false according to question (given P(x)= False for all x ∈ S) then there won’t be any problem because then False→ anything will be true for a also.

 

---

@ASNR1010 @Deepak Poonia Sir what “<=” denote ?? any binary operation or specifically “less than ”operation??

---

@abir_banerjee it is indicating that relation is POR 

Answer 1

I’ll try explaining in the easiest and intuitive way.

Let us divide the explanation into three parts.

part 1] Given data

part 2] How to interpret the given data

part 3] Finally reaching the solution.

Part 1] Given data

• S={a,b,c}
• POSET[S,$\leq$] such that ‘a’ and ‘b’ are the minimal element. And ‘c’ is the maximum element. (wait for it :p)
• It is also given that P is as follows:

• The last information is that all (x,y) ∈POSET satisfy x → y (implication).

Part 2] How to interpret the given info

• What are maximal and minimal element?

           Maximal element ‘z’ of POSET[S,$\leq$] is an element in the set S such that there exists no element ‘y’ such that (z$\leq$y)

exists.

Similarly, Minimal element ‘z’ of POSET[S,$\leq$] is an element in the set S such that there exists no element ‘y’ such that (y$\leq$z)

exists.

• Hence using above definitions we can draw the Hasse diagram as follows:

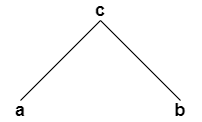
• We know that POSET means ‘Reflexive’, ‘Anti-Symmetric’ and ‘Transitive’ relation.
• Hence using the Hasse diagram and the definition we can conclude that our POSET[S,$\leq$] = { (a,a)  (b,b)  (c,c)  (a,c)  (b,c) }
• And all these pairs have to satisfy x →y as mentioned in the question. We know P(a)=true and P(b)=false.

              

• Now what can be ‘?’. Yes it has to be ‘TRUE’ to satisfy the implication condition. Hence

             

Part 3] Finally reaching the solution

• A. True, since ‘a’ and ‘c’ are both true.
• B. True, since ‘b’ is false.
• C. True, since only (b,b) satisfies the given condition and ‘b’ is false.
• D. False, because only x=c satisfies the condition and we know c is true.

Hence, the answer is D.

Answer 2

•  a and b are minimal.
• c is maximum.
• P(a) is true and P(b) is false.
• If x≤y, then p(x)⇒p(y)

element relates to a, that has to be true

so optiod d is wrong

reason p(x) is false under condition a≤x which is wrong