We will be getting two different grouping..
Grouping $1: (9,8)$
 $\text{SOP}: 2 + 3 + 3 = 8$
$\text{SOP}: 2 + 3 + 3 = 8$
 $\text{POS}: 2 + 2 + 2 + 3 = 9$
$\text{POS}: 2 + 2 + 2 + 3 = 9$
GROUPING $2: (9,10)$
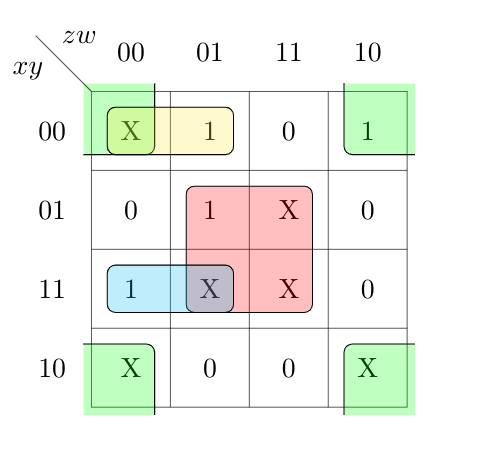 $\text{SOP}: 2 + 2 + 3 + 3 = 10$
$\text{SOP}: 2 + 2 + 3 + 3 = 10$
 $\text{POS}: 2 + 2 + 2 + 3 = 9$
$\text{POS}: 2 + 2 + 2 + 3 = 9$
Both the grouping are correct representation of the function $f(wxyz)$
PS: Some wrong beliefs about don't cares
- "once you have assumed a don't care as '1' u can't use the same don't care for grouping zeros and vice versa"
- "if don't care has been used in POS than can't be used in SOP"
Both these statements are wrong. Don't care simply means just don't care -- say we use don't care $d3$ for grouping $1$ in SOP we can use $d3$ for grouping 0 in POS. (The literals in SOP and POS may not be the same)
K-Map grouping is not unique. And the question says about minimal literals. So, the best answer would be (9,8) Since there is no option in GATE we can go with $(9,10)$ (the question setter might have missed Grouping 1)