GATE CSE 1988 | Question: 4ii

Question

Using binary full adders and other logic gates (if necessary), design an adder for adding $4$-bit number (including sign) in $2’s$ complement notation.

Answer 1

Overflow condition in $2's$ complement number system:-

1. $c_{3} = 1,c_{4} = 1\implies$ No overflow
2. $c_{3} = 0,c_{4} = 0\implies$ No overflow
3. $c_{3} = 1,c_{4} = 0\implies$ Overflow $(a_{3} = b_{3} = 0)$
4. $c_{3} = 0,c_{4} = 1\implies$ Overflow $(a_{3} = b_{3} = 1)$

We can conclude that the overflow condition for $2's$ complement number system is: $$c_{3}\oplus c_{4} = 1\\ \text{(OR)} \\ \bar{a_{3}}\cdot \bar{b_{3}}\cdot s_{3} + a_{3}\cdot b_{3}\cdot\bar{s_{3}} = 1$$

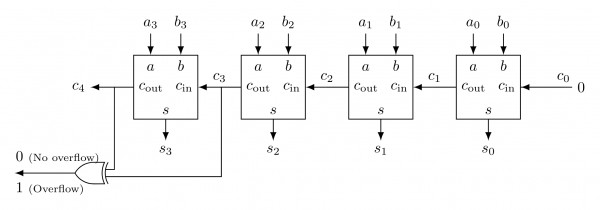
Here, we used $4-bit$ binary full adder and Ex-OR gate.

The Ex-OR gate is used to check the overflow condition.

Comments

The OR part of overflow condition is wrong. please correct it.

---

What's wrong with that?

---

$\bar{a_3}⋅\bar{a_3}⋅s_3+a_3⋅b_3⋅\bar{s_3}=1 $

this will be a'b's+abs' =1

---

okay I will corrected

---

@Lakshman Patel RJIT

What do you mean by "design an adder for adding 4-bit number (including sign) in 2’s complement notation." (Highlighted one)?

---

It means take 2 numbers then convert them to 2's complement form and then add them using adder

---

@Satbir

What happen if we do same thing in 1's complement form or sign magnitude form?

---

you can try to design circuit for that cases with simiilar approach as given in answer.

---

@satbir how have you derived this condition for the overflow?

---

@PratikDey0316

I think, for the second part of the overflow condition it basically says that, since a3 and b3 bits are sign bit so if two positive number are being added(sign bit is 0) then their result cannot be negative(s3 cannot be 1), Similarly, when two negative numbers are being added(sign bit is 1) then their result cannot be positive(s3 cannot be 0). If I am wrong here then please correct me.

As for the first part of the overflow condition you can refer this link: http://sandbox.mc.edu/~bennet/cs110/tc/orules.html

 

---

Hoping that somebody finds it useful –

In case of \(2\)’s complement representation, overflow happens only when adding two \(n\)-bit numbers, both having the same sign (there won’t be an overflow anyway when the numbers are of opposite sign) produces a \(n\)-bit result (ignoring the carry generated from the addition, if any) of the opposite sign. So, \(a’_n.b’_n.s_n+a_n.b_n.s’_n=1\) iff

1. adding two non-negative numbers (i.e., sign bits are \(0\), or, \(a’_nb’_n=1\)) produces a negative number (i.e., sign bit is \(1\), or, \(s_n=1\)), or,
2. adding two negative numbers (i.e., sign bits are \(1\), or, \(a_nb_n=1\)) produces a non-negative number (i.e., sign bit is \(0\), or, \(s’_n=1\)).

Answer 2

The Ex-OR gate is used to differentiate b/w normal binary addition vs 2’s complement addition.

ref:- https://www.ijert.org/efficient-design-of-2s-complement-addersubtractor-using-qca-2

Comments

This is subtraction using adder not addition of two numbers.

---

both addition and subtraction can be performed using this ,using the value of c_in

---

Cin = 0 for normal 4 bit addition correct that line