They are asking to convert Complete Undirected graph into Directed graph without cycle by choosing direction for the edges.
See this $K_{3}$ graph-
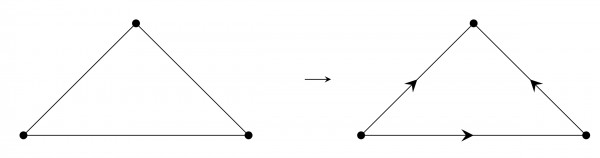
(Image ref)
By this time you must have got the problem statement meaning- our resultant graph should be acyclic.
Lets say we have a complete graph $G$ which has $n$ vertices, $v_1, v_2,\dots v_n$. To convert it into the resultant graph we have to assign direction to each edge. Now see, our resultant graph is acyclic therefore it must have a topological order.
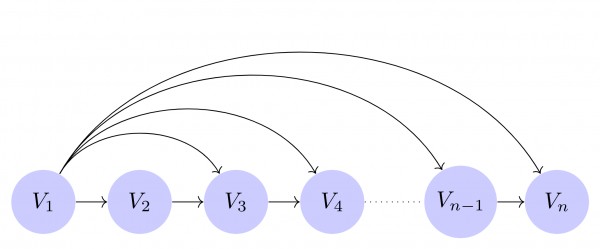
(I have not drawn all edges except $V_1$ edges.)
here every rearrangement of vertices in topological sort leads to one particular combination to choose the direction of edges.
Hence - $n!$ is answer.
Just to illustrate more, see one of the permutation out of $n!$
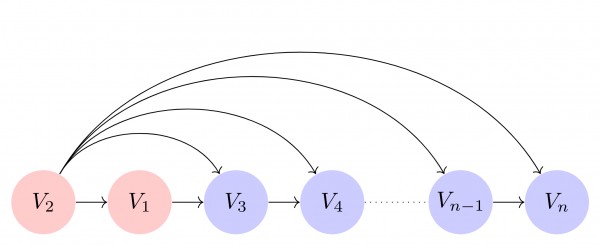
These two permutation shows that undirected edge between $V_1$ and $V_2$, was first chosen as $V_1 \rightarrow V_2$ and then $V_2 \rightarrow V_1$
Don't think about the labeling of vertices, If I do unlabelling of all $n!$ permutations then all structures are same. But it doesn't matter If I am arriving at the same structure, What matters is, In how many ways I can reach to that.
See this-
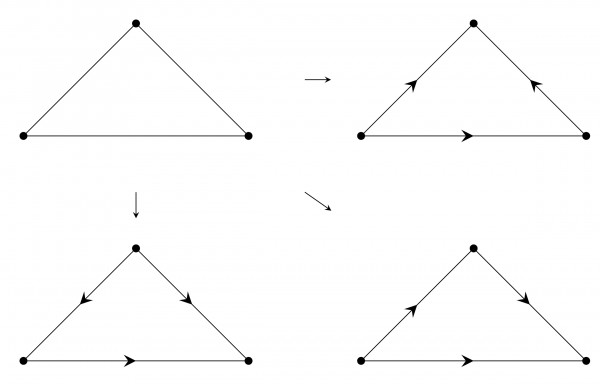

All the above $3$ structures are Isomorphic. But still, there are $3!$ ways to reach such structure.
Let there be $3$ vertices,
In how many ways we can arrage them? It is $3! = 6$
- $a,b,c$
- $a,c,b$
- $b,a,c$
- $b,c,a$
- $c,a,b$
- $c,b,a$
Let's take each order, and check in how many ways we can make it as directed edges ( remember there are 3 edges in K3 ) with it
ex :- $b,a,c:$ we make $b \to a \to c.$ Now the remaining edge must be $b \to c;$ there is no other possibility for it, as if we make $c \to b$ then it is cyclic.
So, there is only one way to assign edges, to each order !
Now, you got doubt that " There may be many assignment of direction of edges than permutations ? "
Answer for this question is, Should be NO. ( think about it, let there be an edge $u \to v,$ then $u$ should be before $v$)
In how many ways we can choose direction for the edges so that there are no directed cycles? $\to$ Number of permutations of vertices $= n !$
Correct Answer: $C$