Answer is D.
To be able to store " any " binary tree on n vertices the minimum size of X should be
" Any Binary Tree and Size should be minimum " .
So We must consider worst case binary tree for this situation and find the minimum space required .
Minimum size for $\underline{\text{any}}$ binary tree
$\implies$Minimum size of worst case binary tree
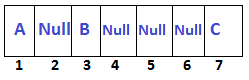
$\qquad {X[i] = node \\ X[2i] = \text{Left child} \\ X[2i+1] = Right child}$
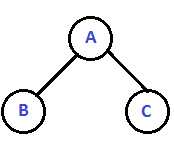
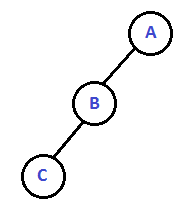
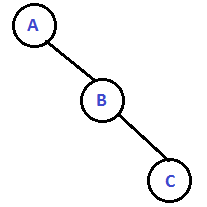
Let $n = 3$
|
|
|
|
|

|

|
|
$X[1] = A $
$X[2] = B $
$X[3] = C$ |
$X[1] = A$
$ X[2] = B$
$ X[4] = C$ |
$X[1] = A$
$ X[3] = B$
$ X[7] = C$ |
| $n$ |
$2^{n - 1}$ |
$2^n-1$ |
| Minimum size Best Case binary tree |
|
Minimum size Worst Case binary tree |