Matching number of a graph is defined as the maximum number of non-adjacent edges in a graph.
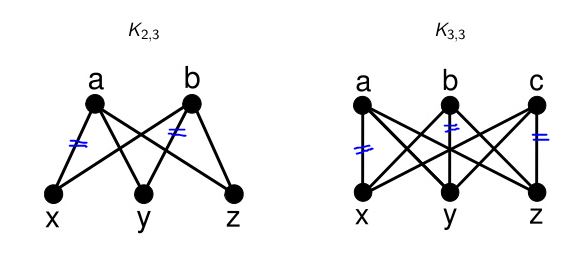
(I have marked one maximum-possible set of non-adjacent edges, but other set is also possible)
In a complete bipartite graph $K_{m,n}$ $m$ nodes are adjacent to each of the $n$ nodes and $n$ nodes are adjacent to each of $m$ nodes. (basic definition of bipartite graph)
So, If an edge is to be included in counting of Matching number, then all adjacent edges cannot be included.
So, Matching Number in $K_{2,3} = 2$ and in $K_{3,3} = 3$
Although there may exist a much formal proof, but by taking few more examples it can be said that Matching Number for $\color{maroon}{K_{m,n} = \;min(m,n)}$