A. $n_0(s)$ is a $3$ digit prime. It means no. of $0's$ are in the range (set) $\{101,103,\ldots,997\}$ which is finite. So, $L$ will be regular.
For simplicity consider $n_0(s)$ is a $1$ digit prime. So set will be $\{2.3.5.7\}.$ DFA will look like
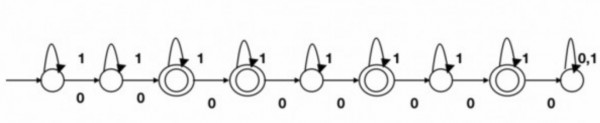
B. Prefix - For a string $s,$ its prefix $s'$ is any substring from the beginning of $s.$
Example: $s = 10110, s' = \{1, 10, 101, 1011, 10110\}.$
$L=\left\{ s \in (0+1)^* \mid \text{ for every prefix s' of s,} \mid n_{0}(s')-n_{1}(s') \mid \leq 2 \right \}$
So, here we have to ensure that no where in our string the difference between number of $0's$ and $1's$ is greater than $2.$ If anywhere the above condition fails, we will enter a dead state as we got a substring (prefix) that violates the condition.
DFA will be like
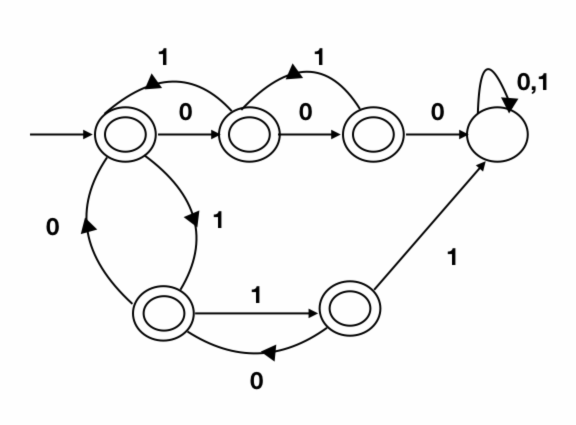
So, here the difference between number of $0's$ and $1's$ crosses $2$ we will be in dead state.
e.g., $s=10110, s' = \{1, 10,101,1011,10110\}$
This string will be accepted as nowhere in $s'$ the difference exceeds $2$.
$s=011110, s'=\{0,01,011,0111,\underbrace{01111}_{\text{diff} = 3},011110\}$
This string is not accepted.
C. The difference between the number of $0's$ and $1's$ should not exceed $4.$
Here, once we exceed the limit there is a possibility that we might cover up the difference in further part of the string.
e.g., $0111111000$
Here, just by seeing up to the last $1$ we cannot move to dead state. So, it needs infinite counting. Hence, not regular.
D. This language can be stated as the set of strings where number of $0's$ is divisible by $7$ and number of $1's$ is divisible by $5.$ We can make a DFA for this by cross-product method. Hence, regular.