ISRO-DEC2017-5

Question

Let $f(x)=\log|x|$ and $g(x) =\sin x$. If $A$ is the range of $f(g(x))$ and $B$ is the range of $g(f(x))$ then $A\cap B$ is

• A. $[-1,0]$
• B. $[-1,0)$
• C. $[-\infty ,0]$
• D. $[-\infty ,1]$

Comments

Is it option A?

---

Any explanation??

---

$log \left | sinx \right | range : \left [ -\infty ,0 \right]$

$sin(log\left | x \right |) range : \left [ -1, 1 \right ]$

intersection : $ \left [ -1 ,0 \right]$

Answer 1

f(g(x)) = log|g(x)| =log |sin x|

  

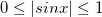
which is given to input for log function

and we know in domain of [0,1] log will give range (- 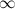 ,0]

so here range of f(g(x)) = (- 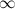 ,0]

g(f(x)) = sin(f(x))  = sin(log|x|)

log|x| will gives values in between - 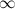 to +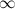 

and which is given the input for sin function

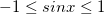
so range of g(f(x)) is [-1,1]

common of both is [-1,0]

Answer 2

I think it should be A as the log|sinx| { |sinx| vary from 1 to 0 } so range of log|sinx| is -inf to 0
for sin(log|x|) we have log|x| range over Real number so sin(x) range over -1 to 1 and hence intersection is
[-1,0]