The following table gives the cost of transporting one tonne of goods from the origins A, B, C to the destinations F, G, H. Also shown are the availabilities of the goods at the origins and the requirements at the destinations. 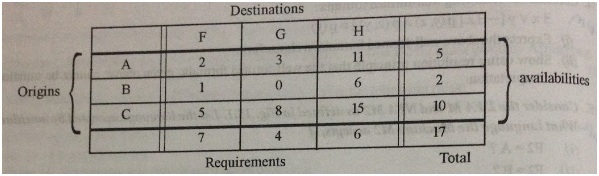
The transportation problem implied by this table can also be written in the form
$$\text{minimize} \: \: \underline{c} \: ^T \: \underline{x}$$
$$\text{subject to :} \: \: Ax= \underline{b}$$
$$ \underline{x} \geq 0$$
Display $\underline{c} \: ^T , A$ and $\underline{b}$ if $\underline{x}$ is the vector
(XAF, XAG, XAH, XAH, XBF, XBG, XBH, XCF, XCG, XCH)
Where $x_{ij}$ represents the shipment from $i$ to $j$.