Let T be a depth-first search tree in an undirected graph G. Vertices u and ν are leaves of this tree T. The degrees of both u and ν in G are at least 2.
Let's interpret question correctly and draw inferences
Vertices u and ν are leaves of this tree T.
Means (1) (u,v) is not an edge in the graph otherwise one would have been descendent of another and both of them must not be leaves.
(2) If vertices u and v are leaves of tree T, then when DFS was exploring them, after exploring say vertex u, it was unable to find any new unvisited Neighbour of u and hence, it had to backtrack the search. So, u became leaf of T. Same story goes with vertex v.
(3)If degrees of vertices u and v are at least 2 then I say consider the scenario for vertex u
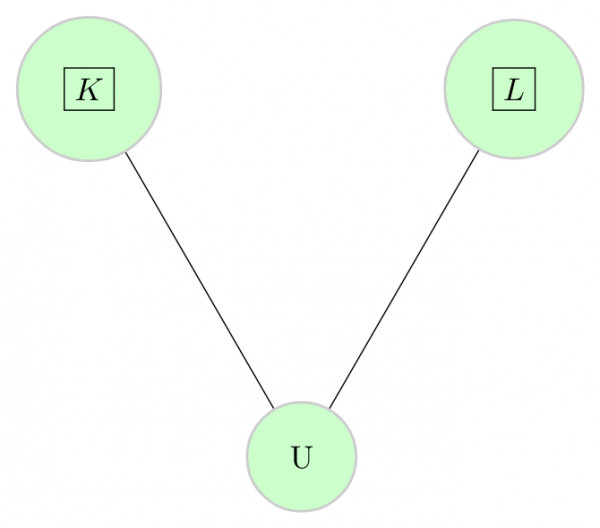
Consider some intermediate vertices K and L which are neighbours of vertex U, and there may be more vertices than K and L, ahead of them connected to either one of them(to K or L) but for simplicity, I consider only two(K and L).
Now, say my DFS algorithm explored vertex K, coloured it, Grey, then it went to vertex U and found it WHITE (means unvisited) so it marks it Grey and makes the edge (K,U) a tree edge. Now DFS examines neighbour of U and finds neighbour L.
Now if the neighbour L was WHITE (Means not visited), DFS would have visited this vertex L and then edge (U,L) would have been marked as tree edge and in this case Vertex, U would no longer be a leave in DFS Tree T.
So, Necessarily my vertex L was visited before U (L Maybe GREY or BLACK in colour) and this would have been connected to vertex K via some other vertices or directly, otherwise, it was impossible for this vertex L to be discovered via path any other than from U to L.
So, what all this means?
Yes Vertex U and it's neighbour are in a cycle and your DFS will mark some edges as back edges.
The similar story would hold for vertex V.
So, even if Option had said
"Vertex U and V are involved in cycle with their neighbour" then also this would have been true.
So Option (D) is the answer.