GATE CSE 2014 | Set 3 | Question: 39

Question

Suppose we have a balanced binary search tree $T$ holding $n$ numbers. We are given two numbers $L$ and $H$ and wish to sum up all the numbers in $T$ that lie between $L$ and $H$. Suppose there are $m$ such numbers in $T$. If the tightest upper bound on the time to compute the sum is $O(n^a\log^bn+m^c\log^dn)$, the value of $a+10b+100c+1000d$ is ______.

Comments

Can it be done this way?

A hash table of size H can be initialized. // O(H) Space, let the table be Arr[H+1]
Next, all of the nodes till the target node can be marked visited in the table. O(logn) for 2 searches. (Remember, the nodes shall be only marked visited if were not visited before, to get rid of duplicate entries).
Finally, the hash table can be traversed, and the visited node’s sum can be calculated. // Start visiting from Arr[L]
Time Complexity : O(m+logn).
Auxiliary Space: O(H).

---

GO Classes link

Hope this helps !

---

Thanks for the explanation link video.

Answer 1

In worst case for finding $L$ and $H$ it will take $O(\log n)$ time as the given tree is balanced binary search tree.
Now there are $m$ elements between $L$ and $H$. So to traverse m element it will take $O(m)$ time (traversal algorithm given below). So, total

$O(m+\log n)  \implies a=0, b=1,c=1,d=0$
$\therefore 0+(10 \times 1)+(100 \times 1)+(1000 \times 0)=110$. 

---

To find all the numbers from $L$ to $H$ we can do an inorder traversal from root and discard all elements before $L$ and after $H$. But this has $O(n)$ time complexity. So, we can do a modification to inorder traversal and combine with binary search as follows:

1. Find $L$ using binary search and keep all nodes encountered in the search in a stack. 
2. After finding $L$ add it to stack as well and initialize $\text{sum} = 0$.
3. Now, for all nodes in stack, do an inorder traversal starting from their right node and adding the node value to sum. If $H$ is found, stop the algorithm. 

Comments

@Krishna Reddy kyp we are not assuming we are calculating it using O(m) . And why we can do that the reason is simple its BST so inoder is simple ascending order . Now we are asked to sum elements between L and H hence we just need to do in oder traversal from L to H going through M ele thus taklinh O(m).

 

---

This is a repeated question

https://gateoverflow.in/333190/gate-cse-2020-question-41

---

@Krishna Reddy kyp inorder for worst case  we chose element  L and H from leaf 

Answer 2

Here is an example 😊

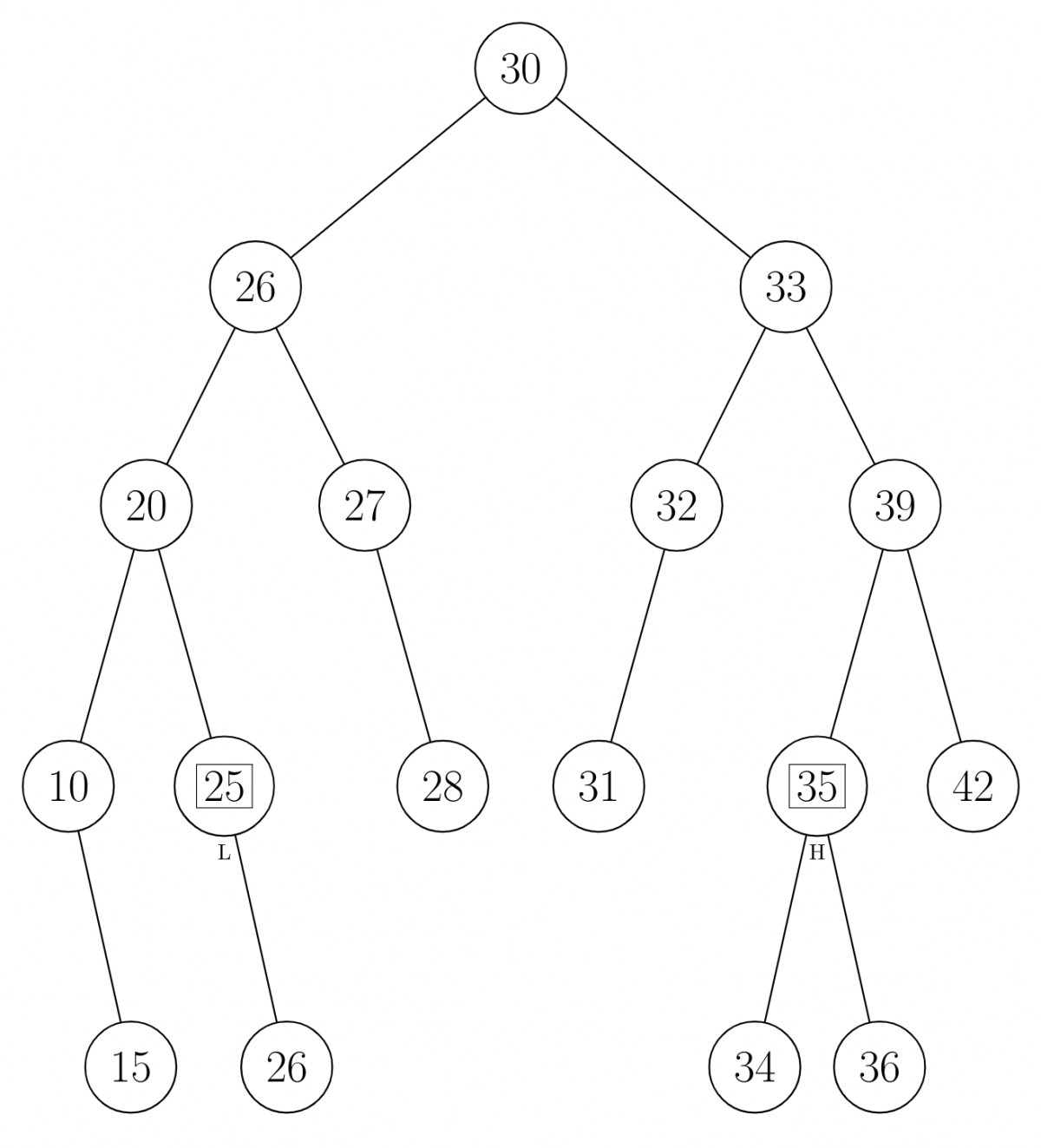
$L =25 , H = 35$
Inorder: $10,15,20,\underset{L}{\boxed{25}},26,27,28,30,31,32,33,34,\underset{H}{\boxed{35}},36,39,42$

1. Find $L$ and $H \rightarrow O(\log n)$ time.
2. Traverse '$m$' elements between '$L$' and  '$H$' $\rightarrow O(m)$ [Traversal algorithm]

Total $\rightarrow  O(m + \log n) $

$\qquad a= 0,b=1,c=1,d=0$

$\qquad 10 + 100 = 110$ Answer

Traversal Algorithm:

1. Find $L$ using Binary search and keep  $H>node> L$ encountered in the search in a stack.
   
2. After finding $L,$ add it to stack as well & initialize $sum = 0$
3.  Now, for all nodes in the stack, do an inorder traversal starting from their right node and adding the node value to sum. If it is found than stop the algorithm.

• Node (1) 
  • No Right child; Sum = Sum + Node value $= 0 + 25 = 25.$
• Node (2)
  • Inorder Traversal from Right Child $\rightarrow  24,28$
  • Sum = sum + inorder Traversal + Node Value $=  (25 + 27 + 28) + 26$
• Node (3)
  • Inorder Traversal From Right Child $\rightarrow 31,32,33,34,\overset{H}{\bf{35}}\overset{\to \text{Stop Inorder Traversal}}{}$
  • Sum = Sum + Inorder Traversal + Node value
    • $\qquad = 25 + 26 + 24 + 28 + (31 + 32 + 33 + 34 + 35) + 30$
    • $\qquad = 25 + 26 + 24 + 28 + 30 + 31 + 32  + 33 + 34 + 35$  Answer

---

EDIT :

1. In Step 1, we need to find only $L$ and not $H.$
2. In Traversal Algo: Find $L$ using Binary Search and Keep, L< Nodes< H, encountered in the search in the stack.

Comments

Thank you for this

---

Node 1 has right child 26.But why you mentioned there is no right child and took sum as 0+25?

---

@VS please make an edit to your answer in the inorder of node2 in the stack. It will not be 27,28 instead of 24,28. This mistake creates more confusion in the already complex algorithm. 

Answer 3

int getSum(node *root, int L, int H)
{
   // Base Case
   if (root == NULL)
      return 0;

   if (root->key < L)        
       return getSum(root->right, L, H);

  if (root->key > H)
      return getSum(root->left, L, H)

   if (root->key >= L && root->key <=H)        
      return getSum(root->left, L, H) + root->key +
             getSum(root->right, L, H);
}

it will be O(logn +m)

it can go max of logn depth to find nodes in range and  function calls for nodes in range ie m

Note that the code first traverses across height to find the node which lies in range. Once such a node is found, it recurs for left and right children. Two recursive calls are made only if the node is in range. So for every node that is in range, we make at most one extra call (here extra call means calling for a node that is not in range).

source:http://geeksquiz.com/gate-gate-cs-2014-set-3-question-49/

Comments

Thanks for valuable effort.

---

So in worst case 'm' can equal to 'n', right?

---

# Please look into this.

def inorderTraversal(self, root, L, H):
        tot_sum = 0
        stack = []
        cur = root
        while stack or cur:
            if cur:
                stack.append(cur)
                cur=cur.left
            else:
                cur=stack.pop()
                if cur.val >= L and cur.val <= H:
                    tot_sum += cur.val
                cur=cur.right
        return tot_sum

 

What about my code. 

Its O(n) and the sum is directly calculated. In worst case m = n, so your algorithm O(m + logn) will be same as mine. Doesn't the ques ask about the worst case.

Answer 4

Do tree traversal from root as follows: Do a recursive search to find L, saving all the nodes visited in a stack. Since tree is balanced BST, it'll take O(log n) time. After finding L instead of search do inorder traversal up to m nodes from this node and continuing (if needed) using the saved nodes during searching. Complexity O(m).

Total time = O(m) + O(log n)

a=0, b=1, c=1, d=0
a+10b+100c+1000d = 0+ 10 + 100 + 0
= 110

Comments

@Rajesh Pradhan sir, I have the same confusion. Have you got it now? Why is stack required here?

Just in case you read this, can this problem be solved by just finding L $[O(logn)\ time]$, then performing an inorder traversal for m+1 numbers $[O(m)\ time]$; then adding them up $[O(1)\ time]$

My point is, can it be solved simply like that, or am I missing something?

---

@JashanArora adding to your points, I think your approach is valid we just need to make sure that the values < L in inorder traversal must be dropped. Finally according to me we can solve it without using stack in the following way:

 

1. First find the value of L.

 

2. Now

IF  L has right node then initialise sum = L  ELSE sum = 0.

 

3. Now

IF  if L has right node do inoder traversal starting from the L's right node and keep on incrementing sum (making sure visited node values are >=  L if not then ignore those values ) with visited node value until we reach H. 

 

ELSE L itself is the right node so start inorder traversal from L itself and keep on incrementing sum ( again making sure visited node values are >=  L if not then ignore those values ) with visited node value until we reach H.

 

4. finally sum value is our answer.

 

@DigvijayPandey sir, @Arjun sir or anyone please correct me if I am wrong.

---

@Aadesh

This is wrong how can you do in-order traversal starting from L, as L will contribute a sub-tree of the whole. That’s why stack is needed to store the nodes that were visited before L.

And instead of ignoring values that are smaller than L , just do the in-order traversal of right-subtrees

Answer 5

within those m numbers, we have to search m times to see if the numbers are existing in the Balanced BST & add them.

so, m log n time.

c = 1, d = 1 => answer = 0 + 0 + 100 + 1000 = 1100

Comments

out of n elements u r checking for exactly m elements.. but it may b possible m-k elements satisfy condition(less than H greater than L).. For rest K elements again u have to do same thing.. that ll take O(n) time..

---

@Digvijay

   U r saying "it may b possible m-k elements satisfy condition(less than H greater than L).. For rest K elements again u have to do same thing.. that ll take O(n) time.."

But in the question  it is clearly mentioned  that there are  'm' such numbers. So how will it be m-k . ?

Can u  please explain it.

Answer 6

I have found an alternative solution, with ref to Coreman textbook exercise, Q.12.2-8. 

If you can prove this (solution: https://stackoverflow.com/questions/40561235/time-complexity-of-finding-k-successors-in-bst)
Then we know that since there are m nodes having value between L and H. We can also say that ‘m’ inorder successors of  node with value ‘L’.
So searching for L : O(log n)
‘m’ inorder successors : O(m+h) = O(m + log n) 
So overall time complexity : O(m + log n). a=1,b=1.c=1,d=0
Answer : 110.

Comments

Best insight with reference!