- PRE ORDER$:1,2,3,4,5,6,7,8,9,10,11,12$
- POST ORDER$:3,5,4,2,7,8,6,10,11,12,9,1$
We can draw the tree, but in the question it is not specified if it is binary or ternary or something else.
Lets assume it is a binary tree.
Pre oder: Data, Left, Right (First node should be root)
(First node should be root, next to the root node should be left node of root, if in the post-order it is not in the second last position)
Post order: Left, Right, Data
(Last node should be root, before the last node it should be right node of root, if in pre-order it is not in the second position)
Now we can conclude that $9$ is right of $1$ and $2$ is left of $1.$
- PRE ORDER $:1,{\color{Red} {2,3,4,5,6,7,8}} ,{\color{Green}{9,10,11,12}}$
- POST ORDER $:{\color{Red} {3,5,4,2,7,8,6}},{\color{Green} {10,11,12,9}}$,1.
We can clearly observe that, the right of root contains $9,10,11,12 \implies$ we can leave $9$ as its position is fixed as immediate right of root.
So remaining elements are $10,11,12.$
What is pre-order of those elements ?
What is the post order of those elements?
Is it possible in Binary Tree? (check all $5$ trees which can formed by $3$ nodes)
NO
Now lets consider a Ternary Tree
- PRE ORDER $:\overbrace{\boxed{1}}^{\text{root}},\overbrace{2,3,4,5,6,7,8,9,10,11,12}^{\text{non-root elements}}$
- POST ORDER $:\underbrace{3,5,4,2,7,8,6,10,11,12,9}_{\text{non-root elements}},\boxed{1}$
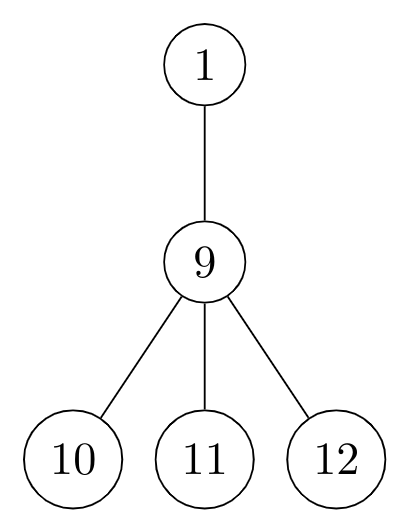
$2$ is left most and $9$ is right most, the children of $9$ are $10,11,12$ from left to right.

- PRE ORDER : $2,3,4,5,6,7,8,9,\overbrace{\boxed{10,11,12}}^{\text{subtree of 9, but order unknown}}$
- POST ORDER : $3,5,4,2,7,8,6,10,11,12,\overbrace{\boxed{9}}^{\text{Right most child of root}}$
Check all the elements in the preorder after $9-$ those should be children of $9.$
After checking the preorder and postorder we can conclude that all those elements are at the same level in the order $10-11-12.$
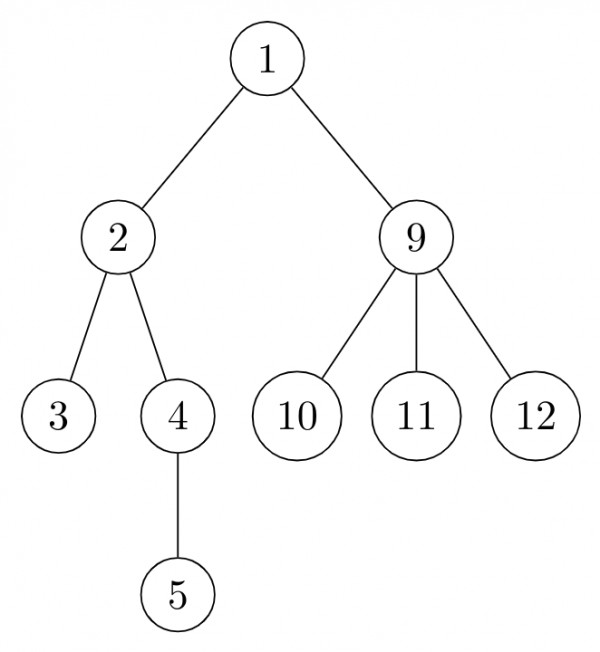
- PRE ORDER : $\overbrace{\boxed{2}}^{\text{Should be the leftmost child of root}\\\text{Elements before 2 in the postorder}\\\text{must be children of 2} },3,4,5,6,7,8$
- POST ORDER : $\underbrace{\boxed{3,5,4}}_{\text{Should be a subtree of $2$}\\\text{but order in unknown}},2,7,8,6$
How we separated $3,4$ and $5$ as two parts?
Check the preorder: $3\implies$ elements before $3$ in the postorder are in the same subtree as $3$ but there are no elements before $3.$
Therefore $3$ is separated from $4$ and $5.$
How we fixed $4$ and $5$ in that order?
Check the preorder: $4\implies$ elements before $4$ in the postorder are in the same subtree of $4.$ Therefore $5$ is in the same subtree of $4.$
- PRE ORDER : $6,7,8$
- POST ORDER : $\underbrace{\boxed{7,8}}_{\text{Should be a sub-tree of 6}\\\text{but order is unknown}},6$
We can easily understand that $6$ is the child of root. Elements before $6$ in the postorder forms subtree of $6.$
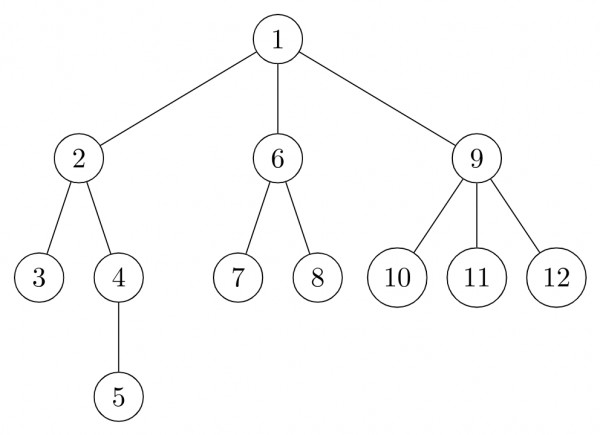
How we fixed $7$ and $8$ in that order?
Check the preorder: $7\implies$ elements before $7$ in the postorder are in the same subtree of $7$ but there are no elements before $7.$
Therefore $7$ and $8$ are separated.