GATE CSE 1998 | Question: 25-a

Question

Free disk space can be used to keep track of using a free list or a bit map. Disk addresses require $d$ bits. For a disk with $B$ blocks, $F$ of which are free, state the condition under which the free list uses less space than the bit map.

Comments

This question is taken from Tanenbaum’s Modern Operating Systems, from the File Systems chapter.

---

The bit map requites $B$ bits. The free list requires $D \times F$ bits.

The free list requires fewer bits if $DF < B.$

Alternatively, the free list is shorter if $(F/B) < (1/D)$ , where $(F/ B)$ is the fraction of blocks free.

Answer 1

Bit map maintains one bit for each block, If it is free then bit will be "$0$" if occupied then bit will be "$1$".
For space purpose, it doesn't matter what bit we are using, only matters that how many blocks are there.
For $B$ blocks, Bit map takes space of "$B$" bits.

Free list is a list that maintains addresses of free blocks only. If we have $3$ free blocks then it maintains $3$ addresses in a list, if $4$ free blocks then $4$ address in a list and like that.

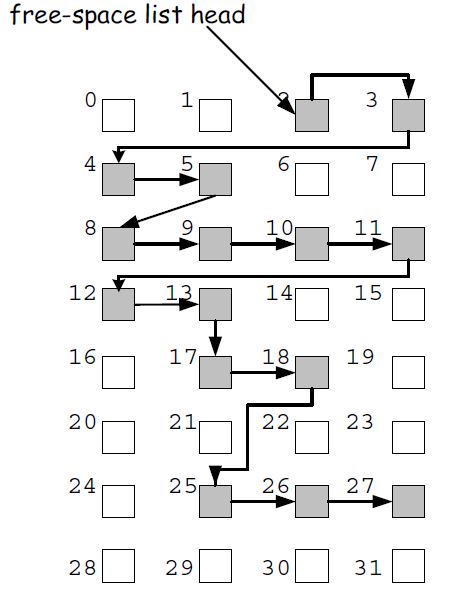
Given that we have $F$ free blocks, therefore $F$ addresses in a list, and each address size is d bits therefore Free list takes space of "$Fd$".

condition under which the free list uses less space than the bit map: $Fd<B$

Comments

The list will also have pointers pointing to the next element. Why are we not considering the size of these pointers?

---

If anyone has my doubt, the pointer to the next free block is stored in the previous free block in list

---

Anyone please let me know if the below approach is correct:

My attempt)

# of disks = 2$^{d}$

# of blocks free in each disk = F

Total # of blocks in each disk = B

# of bits in block address = log B

 

1) Bit map implementation: We just need B-length string for each disk. So, bit map size = 2$^{d}$ $\times$ B

 

2) Free list implementation: We have to maintain free block address of all free blocks.

We require (d + log B) bits to address a free block in a disk and there are 2$^{d}$ $\times$ F free blocks in total.

So, free list size = 2$^{d}$ $\times$ F $\times$ (d + log B)

 

For, free list to occupy less size than bit map, we need to have 2^d $\times$ F $\times$ (d + log B) < 2$^{d}$ $\times$ B

Canceling the common terms that would give, F $\times$ (d + log B) < B

Answer 2

Solution for Part a :-

Assume that size of each block is S bits.

Then no of bits required for free list is = Fd, No of blocks required = Fd/S

No of bits required for Bit map = B (No of blocks ) , No of block required is =  B /S

Condition under which free list uses less space than the bit map.

Fd / S < B / S

Comments

why divide by S ??

in the above selected answer there is no such division and condition FD<B is sufficient i think ?

explain your approach please .

---

@nikunj he just explained in terms of disk blocks assuming size of each block to be S bits. 

Answer 3

Freelist is used to store list of those addresses which are free