A full binary tree of $8$ leaves
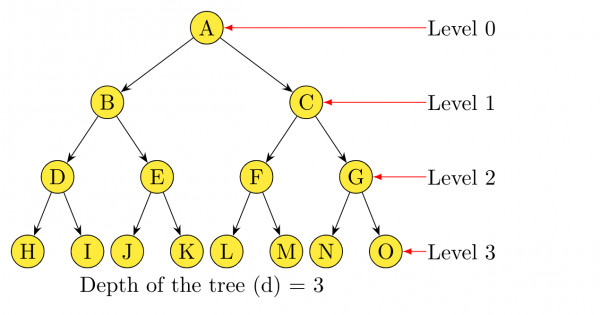
Let's say we take node $H.$ The distances from $H$ to all other nodes (including itself) would be:
$\begin{array}{|c|c|c|c|c|c|c|c|}\hline
H&I&J&K&L&M&N&O\\\hline
0&2&4&4&6&6&6&6\\\hline
\end{array}$
If another node is taken, a similar table (to the one above) is attained. Therefore, all nodes have the same distances when added together.
So, if a node is considered, the probability of choosing another node would be $1/8$ (including itself - independent choosing].
Therefore, $E = \frac{1}{8} \left[0+2+4+4+6+6+6+6\right] = 4.25$