Madeeasy Algorithm

Question

How to solve this recurrence relation

T(n)= T(0.09n) + T(0.91n) + cn

where c is constant and T(1)=1

options are-

Comments

Correct sir.

---

Thanks @Kabir5454 and @gatecse Sir for pointing out my mistake.

P.S. I have corrected the answer accordingly attaching @Kabir5454 ‘s proof (not sure if I am authorized to copy someone’s comment and put on my own answer after giving his/her credit).

---

You’re welcome @Abhrajyoti00

Of course it depends on the person but no reasonable person will object to sharing his/her education content when due credit is mentioned unless there is a legal restriction (like content being owned by some company).

Also knowledge is supposed to be shared. If you read and understand something, you can always share it in your own words and no copyright applies. 

Answer 1

Answer: Both Option A and Option B.

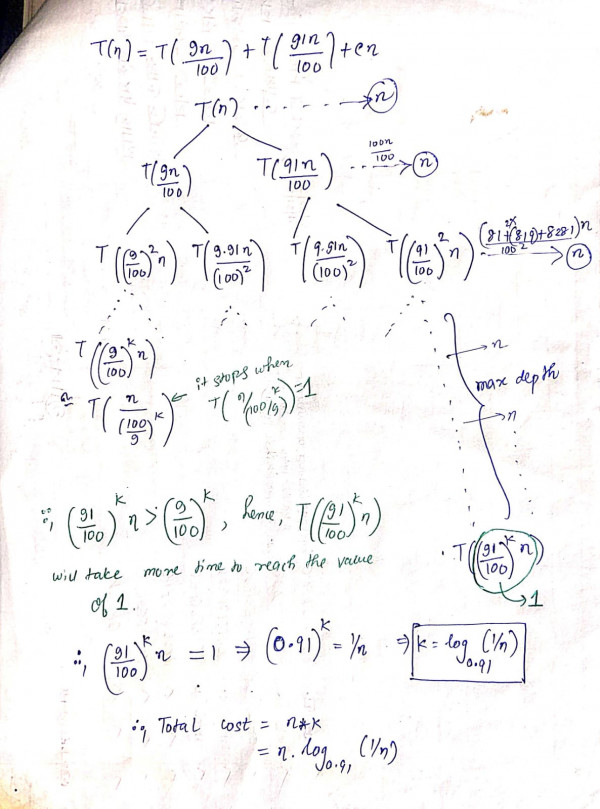
The total cost becomes = $n.log_{0.91}(1/n)$.

Now we can say : $n\log_{0.09}\frac{1}{n}\leq T(n)\leq n\log_{0.91}\frac{1}{n}$

Thus, $O(n.log_{0.91}(1/n))$ and  $\Omega(nlog_{0.09}\frac{1}{n})$

-------------------------------------------------------------------------------------------------------------------------------------------------

Attaching the proof by @Kabir5454 for $\Theta(n.log_{0.91}(1/n))$ or $\Theta(n.log_{0.09}(1/n))$:-

Lets do it formally ,

as already explained $\Omega (n.\frac{\log_{a}n}{\log_{a}\frac{100}{9}})$[ a is some constant base]

$T(n)=O (n.\log_{\frac{100}{91}}n)=O(n.\frac{\log_{a}n}{\log_{a}\frac{100}{91}})=O(n\log_{a}n)$

So,we know ,

$T(n)=Θ(f(n))$ if and only if $T(n)=Ω(f(n)) $ and $T(n)=O(f(n))$ .

So we can conclude ,$T(n)=\Theta(n \log_{a}n).$

This also proof option (B) is true .if we put $a=100/9 .$

 

Comments

Perfect answer👍

So the whole problem was because of $\Theta$ notation  .

just had some doubts here

1. if $option$ $A$ is   $\Theta(nlog_{0.91}(1/n))$  And $option$ $B$ is  $\Omega (nlog_{0.09}(1/n))$
2. if $option$ $A$ is   $O$$(nlog_{0.91}(1/n))$  And $option$ $B$ is  $\Omega (nlog_{0.09}(1/n))$
3. if $option$ $A$ is   $O$$(nlog_{0.91}(1/n))$  And  $option$ $B$ is  $\Theta (nlog_{0.09}(1/n))$

In all the three cases ,  both  $option$ $A$  And  $option$ $B$  are correct right?

---

Yes @Pranavpurkar all of them have both option A and B correct as proved by @Kabir5454

---

Abhrajyoti00

Thanks buddy:)