GATE DS&AI 2024 | Question: 51

Question

Let $\text{u}=\left[\begin{array}{l}1 \\ 2 \\ 3 \\ 4 \\ 5\end{array}\right]$, and let $\sigma_{1}, \sigma_{2}, \sigma_{3}, \sigma_{4}, \sigma_{5}$ be the singular values of the matrix $\text{M}=\text{u} \text{u}^{\text{T}}$ (where $\text{u}^{\text{T}}$ is the transpose of $\text{u}$ ). The value of $\sum_{i=1}^{5} \sigma_{i}$ is $\_\_\_\_\_\_\_\_\_$

Comments

But they  asked the sum of sigular values know, not sum of eigen values.

Answer 1

Answer is simply the sum of the square of the elements of vector $u.$

So, $\Sigma_{i=1}^{5}\sigma_i = 1^2+2^2+3^2+4^2+5^2=55$

----------------------------------------------------------------------------------------------------------------------------------------

Now, comes to most important thing here. Why ?

The reason is, in SVD, we write the equation as:

$uu^T = U \Lambda U^{-1}$

Where, $\Lambda = \Sigma\Sigma^{T}= diag(\sigma_1^2,\sigma_2^2,...)$

And $\sigma^2= eigen(uu^T)=eigen(u^Tu)$

Sum of eigen values of a matrix is the trace of that matrix.

So, Here, $eigen(u^Tu)=\Sigma_{i=1}^{5}u_i^2=1^2+2^2+3^2+4^2+5^2=55$

Or you can get the answer by finding the trace of matrix $uu^T$ 

Here, $u_i$ represents the elements of vector $u$ and "eigen" represents the eigen values and diag() represents a diagonal matrix with its elements as diagonals.

$\sigma$ is called the singular values.

$\textbf{Proof}:$

Suppose we have a matrix $A \in \mathbb{R}_r^{m \times n}$ where $r$ is the rank of the matrix $A$. It means row space of the matrix $A$ is $\mathbb{R}^n$ and the column space of the matrix $A$ is $\mathbb{R}^m$.

Now, suppose we have to map two orthonormal basis vectors of row space $v_1$ and $v_2$ to two orthonormal basis vectors of the column space $u_1$ and $u_2$. We can do it as:    

$Av_1=\sigma_1u_1$ and

$Av_2=\sigma_2u_2$

Suppose $v_1$ and $v_2$ forms the matrix $V$ and $u_1$ and $u_2$ forms a matrix $U.$ (You can simply generalize this idea to high order matrices)

We can write the above two equations as 

$AV=U\Sigma$

Where

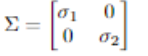
Now, $AV=U\Sigma$ implies $AVV^T=U \Sigma V^T$

Since, $V$ is an orthonormal matrix, so, $V^T=V^{-1}$

$A=U \Sigma V^T$

This is the SVD.

Now, if post multiplied by $A^T$ in $A=U \Sigma V^T$, we get,

$AA^T = (U \Sigma V^T)(U \Sigma V^T)^T$

$AA^T = (U \Sigma (V^T)(V \Sigma U^T)$

$AA^T = U \Sigma (V^TV) \Sigma^T U^T$

Since, $V^T=V^{-1}$ and $V^{-1}V=I$

We get,

$AA^T=U \Sigma \Sigma^T U^T$

Since, $U^T=U^{-1}$, we get the eigen decomposition equation as:

$AA^T=U \Lambda U^{-1}$

Where, $\Lambda = \Sigma \Sigma^{T}= diag(\sigma_1^2,\sigma_2^2,...)$

So, 

$\sigma^2= eigen(AA^T)=eigen(A^TA)$

The reason is that $AA^T$ and $A^TA$ have the same non-zero eigen values.

$\textbf{Proof}$

$AA^Ty=\lambda y$

$A^TAA^Ty=\lambda A^Ty$

$(A^TA)(A^Ty)=\lambda (A^Ty)$

$(A^TA)z=\lambda z$

So, both $AA^T$ and $A^TA$ have the same non-zero eigen values i.e. $\lambda.$ 

Comments

I feel that there is something missing.

When you have written $uu^{T} = U \Lambda U^{-1}$ and in the proof you have written $AA^{T} =  U \Lambda U^{-1}$ I am assuming that you are considering $A$ = $u$. Am I right in this or not ?

Then you have written $\Lambda = diag(\sigma_{1}^{2}, \sigma_{2}^{2}, ...)$, so $\sigma_{i}$ is the singular value of $A$ which is $u$ in our case. Am I right in this or not ?

Then $\sigma^{2} = eigen(u^{T}u)$ saying that square of singular value is eigen value of $u^{T}u$ which also concludes that $\sigma$ is singular value of $u$.

So with this we can conclude that $\Sigma_{i=1}^{i=5} \sigma^{2} = 55$ where $\sigma$ is the singular value of $u$.

In the question they have asked for $\Sigma_{i=1}^{i=5} \sigma$ where $\sigma$ represents the singular value of matrix $M$

---

@redshellspy

$A=U\Sigma V^T$ is the SVD.

where $U$ and $V$ are the orthonormal matrices which have a function of rotation. 

A "circle" in the row space can be mapped to an "ellipse" in the column space of matrix A by using SVD.

Here, $\Sigma=diag(\sigma_1,\sigma_2,...)$

And sum of singular values for matrix $A$ is $\sigma_1+\sigma_2+...$

------------------------------------------------------------------------------------------------------

Now, for the given question  we have $M=uu^T$ and singular values are defined for the matrix $M$ and for that we need to find the sum of singular values.

Here we are considering, $A=u$ (a vector),

We have proved that $AA^T= U\Lambda U^{-1}$ where $\Lambda=diag(\sigma_1^2,\sigma_2^2,...)$

So, we can write the same for the matrix $M$ and vector $u$ as:
$M=uu^T=U\Lambda U^{-1}$ where $\Lambda=diag(\sigma_1^2,\sigma_2^2,...)$

Now, the sum of singular values of matrix $M$ is $\sigma_1^2+\sigma_2^2+...$

where $\sigma_i^2=eigen(uu^T)=eigen(u^Tu)$

So,  for the given vector $u,$ Sum of singular values of matrix $M$ is:

$\sigma_1^2+\sigma_2^2+\sigma_3^2+\sigma_4^2+\sigma_5^2=$ sum of eigen values of matrix $uu^T$

So, you just have to find the sum of eigen values of matrix $uu^T$ or the trace of matrix $uu^T.$

You can also use the fact that $uu^T$ and $u^Tu$ have the same non-zero eigen values. Proof is already given.

Let me know if you have any doubt.

---

You have written

$$ M = uu^{T} = U \Lambda U^{-1}$$

where $\Lambda = diag(\sigma_{1}^{2} \sigma_{2}^{2}, ...)$. Here note that $\sigma_{i}$ is the singular value of matrix $A$ which $u$ in our case.

Now you have written that sum of singular values of $M$ is $\sigma_{1}^{2} + \sigma_{2}^{2} + ...$. Why this is the case ? why does sum of sigular values of matrix $M$ is equal to sum of square of singular value of matrix $u$ ?

---

You have $A=U \Sigma V^T$

Where the diagonal entries of matrix $\Sigma$ are the singular values of matrix $A$.

Now, for the given question, if we are able to write matrix $M=AA^T$ in the same form then we are done.

Now, we can write $M=AA^T=U\Lambda U^{-1}$

where $\Lambda=\Sigma \Sigma^T$

Since the diagonal entries of matrix $\Sigma$ are the singular values of matrix $A$, so the the diagonal entries of matrix $\Lambda$ are the singular values of matrix $AA^T.$

Since, $\Lambda=\Sigma \Sigma^T$ so the diagonal entries of matrix $\Lambda=\Sigma \Sigma^T$ are the squares of the singular values of matrix $A$ i.e. $\Lambda = diag(\sigma_1^2,\sigma_2^2,...)$

Since the diagonal entries of matrix $\Lambda$ are the singular values of matrix $AA^T=M$.

Hence, sum of singular values of matrix M is $\sigma_1^2+\sigma_2^2+...$