(B)Take distance from S
d(U) =1 from S
d(V)=1 from S
So, d(U) - d(V) =0 , d(X) is one shortest distance of the graph
and BFS traversal will not take edge UV
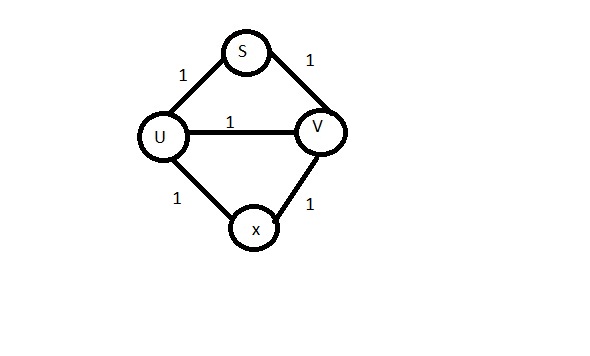
(C) Now for assuming d(U) and d(V) has a distance 1, we similarly calculate the distance from S(in next figure)

(A)In previous figure change the position of U and V, so get
d(U)-d(V) = -1
(D) but 2 not possible as there is a direct edge from U to V always, So, no graph possible with min distance 2. The max distance could be 1
So, ans is (D)