From forouzan tcp/ip protocol suite:
The token bucket algorithm allows idle hosts to accumulate credit for the future in the form of tokens. For each tick of the clock, the system sends $n$ tokens to the bucket. The system removes one token for every cell (or byte) of data sent. For example, if $n$ is 100 and the host is idle for 100 ticks, the bucket collects $10,000$ tokens. Now the host can consume all these tokens in one tick with $10,000$ cells, or the host takes $1,000$ ticks with $10$ cells per tick. In other words, the host can send bursty data as long as the bucket is not empty. Figure shows the idea.
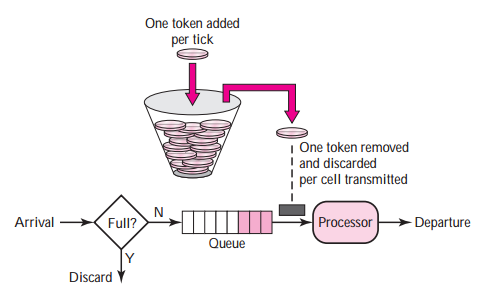
The token bucket can easily be implemented with a counter. The token is initialized to zero. Each time a token is added, the counter is incremented by $1$. Each time a unit of data is sent, the counter is decremented by $1$. When the counter is zero, the host cannot send data.
- The bucket has a capacity. If a host is idle for a long time, then the system will completely fill up the bucket with its maximum capacity of tokens. Token is discarded when bucket is full means
token_counter value in token bucket implementation can not go beyond some capacity value C (predefined)
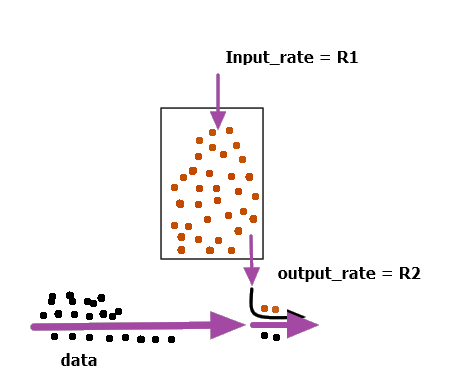
$\begin{align*} &\text{If bucket is full initially with capacity = C} \\ &\text{Then,} \\ &\text{Time to empty the bucket } \\ &T= \frac{C}{R_2-R_1} \\ \\&T = \text{Time for which system can support max data delivery at rate } R_2 \end{align*}$