Testbook Test Series Question

Question

• A. f(A,B,C,D)=∏M(0,1,3,4,5,7,9,11,12,13,14,15) is a max-term representation of a Boolean function f(A,B,C,D) where A is the MSB and D is the LSB. The equivalent minimized representation of this function is

1. (A+C¯+D)(A¯+B+D)(A+C¯+D)(A¯+B+D)
2. AC¯D+A¯BD+A¯BC
3. A¯CD¯+AB¯CD¯+AB¯C¯D¯
4. (B+C¯+D)(A+B¯+C¯+D)(A¯+B+C+D)

Answer 1

find the equivalent min-term which is m(2,6,8,10) 

A¯B¯CD¯+A¯BCD¯+AB¯C¯D¯+AB¯CD¯

= A¯CD¯ + AB¯D¯  (After minimizing)

Now take a=1,b=0,c=0,d=0; and some other values if required

Substitute in the equation above and in the options

In this way i am getting is C .

Answer 2

First try solving K MAP for Maxterms to get minimized expression in terms of POS, as option contains both SOP and POS forms.

Now, Duality does not change the logic of function, We know that POS and SOP are equivalent in terms of functionality. So we can convert

$ \prod \small M ( 0,1,3,4,5,7,9,11,12,13,14,15 )$  to  $\sum \small m (2,6,8,10)$

as for POS we focus on 0 in K MAP or truth table, and in SOP we focus on 1, both above minterms and Maxterms represent the same function. Also, minterm is compliment of Maxterm and vice versa.

Now you can also solve using K-MAP considering SOP by focusing on grouping 1's at respective positions 2,6,8,10 to get minimized SOP expression, just to be sure that we did correctly or not.

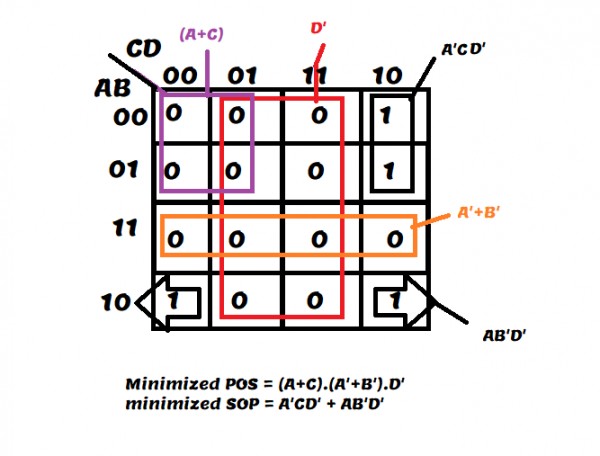
None of the options match unfortunately and question clearly says minimized representation. However, if we look carefully, we can match option C.

A'CD'+AB'CD'+AB'C'D'

Taking AB'D' common from last 2 terms.

A'CD'+AB'D'(C+C')

=A'CD'+AB'D'

Answer 3

Find the product of maxterm of Boolean function F= xy'+x'y'z

Can you solve this unsing distributive law etc

Answer 4

f(A,B,C,D) = m(0,2,6,8,10) =
A¯B¯CD¯+A¯BCD¯+AB¯C¯D¯+AB¯CD¯ =  A¯CD¯(B+B¯) +AB¯CD¯+AB¯C¯D¯ =   A¯CD¯+AB¯CD¯+AB¯C¯D¯

Comments

how can you write max term f(A,B,C,D)= minterm f(A,B,C,D)

the right way is minterm = (maxterm)'

therefore
f(A,B,C,D)=∏M(0,1,3,4,5,7,9,11,12,13,14,15) = [ f(A,B,C,D) = m(0,2,6,8,10) ]'