This code calculates the height of a tree where height starts from $0$
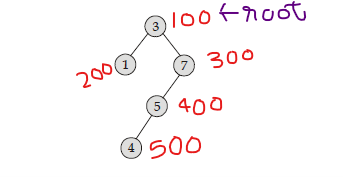
In the daigram I have written address where the respective node are stored.
$root$ stores the address $100$ i.e. points to the root node.
For height(100)
int height Node(*root) //root=100 ,root->left = 200 and root->right = 300
{
if(!100) return -1; // if (0) so condition fails.
if ( 200 && !(300)) return 1+ height(200); //if (200 && 0) = if (0) so condition fails.
if ( !(200) && (300)) return 1+ height(300); //if (0 && 300) = if (0) so condition fails.
return(1+max(height(200),height(300)); // this will execute
}
For height(200)
int height Node(*root) //root=200 ,root->left = NULL and root->right = NULL
{
if(!200) return -1; // if (0) so condition fails.
if ( NULL && !(NULL)) return 1+ height(NULL); //if (0 && 1) = if (0) so condition fails.
if ( !(NULL) && NULL) return 1+ height(NULL); //if (1 && 0) = if (0) so condition fails.
return(1+max(height(NULL),height(NULL)); // this will execute
}
for height (NULL)
int height Node(*root) //root=NULL
{
if(!NULL) return -1; // if (!0)= if(1) so condition satisfied and it returns -1.
....
....
....
}
so $height (NULL)$ returns $-1$ to $height(200)$
$height(200)$ returns returns $1+ max(-1,-1)=1-1=0$ to $height(100)$
So in $height(100)$ we get
return(1+max(0,height(300));
For height(300)
int height Node(*root) //root=300 ,root->left = 400 and root->right = NULL
{
if(!300) return -1; // if (0) so condition fails.
if ( 400 && !(NULL)) return 1+ height(400); //if (1 && 1) = if (1) so condition true calls height(400)
....
....
}
For height(400)
int height Node(*root) //root=400 ,root->left = 500 and root->right = NULL
{
if(!400) return -1; // if (0) so condition fails.
if ( 500 && !(NULL)) return 1+ height(500); //if (1 && 1) = if (1) so condition true calls height(500)
....
....
}
For height(500)
int height Node(*root) //root=500 ,root->left = NULL and root->right = NULL
{
if(!500) return -1; // if (0) so condition fails.
if ( NULL && !(NULL)) return 1+ height(NULL); //if (0 && 1) = if (0) so condition fails. here 0 means false
if ( !(NULL) && NULL) return 1+ height(NULL); //if (1 && 0) = if (0) so condition fails.
return(1+max(height(NULL),height(NULL)); // this will execute and will call height(NULL)
}
for height (NULL)
int height Node(*root) //root=NULL
{
if(!NULL) return -1; // if (!0)= if(1) so condition satisfied and it returns -1.
....
....
....
}
So $height(NULL)$ returns $-1$ to $height(500)$
$height(500)$ returns $1+ max(-1,-1)=1-1=0$ to $height(400)$
$height(400)$ returns $1+0=1$ to $height(300)$
$height(300)$ returns $1+1=2$ to $height(100)$
So in $height(100)$ we get
return(1+max(0,2)); // return(1+2)= return(3)
So $3$ comes as output.