GATE CSE 2021 | Set 2 | Question: 46

Question

Consider the following directed graph:

Which of the following is/are correct about the graph?

• A. The graph does not have a topological order
• B. A depth-first traversal starting at vertex $S$ classifies three directed edges as back edges
• C. The graph does not have a strongly connected component
• D. For each pair of vertices $u$ and $v$, there is a directed path from $u$ to $v$

Comments

k back edges create at least k cycles in the graph. You can find 3 individual cycles in the graph, each cycle has a back edge here.

---

@kruthi-sb 

you are correct to say that '$k$ backedges implies atleast $k$ cycles" but converse of this statement might not need to be true. 

---

@rhl
you're right. thanks for correcting.

Answer 1

Lets put numberings to the nodes as follows:

The back edges are those edges from $v$ to $u$ in set $(u,v)$ where $u$ came first (i.e. already explored) in the DFS tree/forest.

• $3$ to $2$
• $12$ to $11$
• $9$ to $S$

The DFS tree:

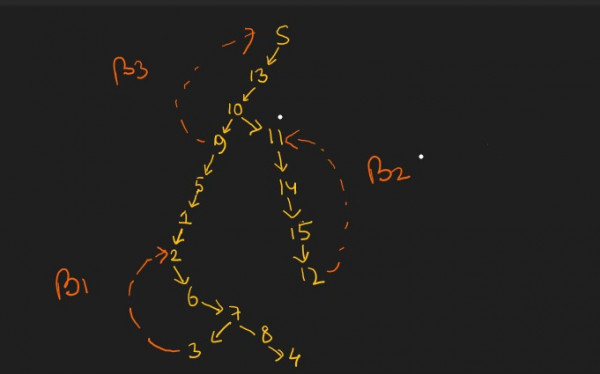
The graph has two cycles one at bottom left and one at bottom right. And every cycle forms SCC (Strongly connected component, since from every vertex $u,$ there is a path to $v, \bf{u \to v})$. C is false

The entire graph doesn’t have SCC. So, definitely D is false. 

Due to the presence of cycles Topological Sort is not possible.

Hence, the answer is A and B.

D would have been correct if it was For some pair of vertices u and v there is a directed path from u to v.

Comments

what is wrong here  ? i got two back edges and third cross edge ?

---

Ya, but it depends how you choose the edges , if we choose 6 first then cross edge else if we choose 9 then we get 3 back edge, and in this problem nodes(vertices) value is not given , we have assumed from 1 to 15 including S

---

Number of back edge means there are cycle if I want to find back edge I just found cycle in graph so watching carefully diagram. (2,3,6,7)  (9,10,13,S)   (11,12,15,14)  these have cycle means back edge will present 3 cycle 3 back edges .

Answer 2

Option A: The graph does not have a topological order. $TRUE$ as there are cycles in the graph which means there are back edges.

Option B: A depth-first traversal starting at vertex S classifies three directed edges as back edges. $TRUE$ as shown in the below image.

Option C: The graph does not have a strongly connected component. $FALSE$ as shown in the below image there are 7 strongly connected components.

Option D: For each pair of vertices u and v, there is a directed path from u to v. $FALSE$ as its not true for all the edges.

So option A & B are correct.

Comments

@Biswajit Kumar can you please explain how you find the cross edge from 
12-6 and 5-11?

---

@Biswajit Kumar @Dknights 
Edges 5-6 and 12-6 might be typos and should not be present in the graph.

Answer 3

A) The graph does not have a topological order , because there’s a cycle in the bottom left corner of the graph

B) Yes, there are only 3 back edges, if started from S.

C) The graph does have a strongly connected component , it has cycle .

D) False , you can observe and find that not all rectangular/square components forms a cycle.

So answer : A) , B)

Comments

My mistake , edited.

---

yes i also got A,B

---

nice explaination

Answer 4

Note: Topological Sorting for a graph is not possible if the graph is not a DAG.

Hence Option(A) is correct

Option(B) is correct .There are 3 back edges from Vertex S  (Back edge: It is an edge (u, v) such that v is the ancestor of node u but is not part of the DFS tree).

Option(D) is incorrect as for each pair of vertices there is not a directed path available

Option(C) is incorrect because Strongly connected component is present in the graph

example of strongly connected graph is