TIFR CSE 2024 | Part B | Question: 9

Question

Given $m$ vectors $\vec{x}_{1}, \vec{x}_{2}, \ldots, \vec{x}_{m}$ in $\mathbb{R}^{d}$, we construct an undirected graph $G=(V, E)$ as follows. Each vector $\vec{x}_{i}$ is represented by a vertex $v_{i}$. We add an edge between vertices $v_{i}$ and $v_{j}$ if the corresponding pair of vectors $\vec{x}_{i}$ and $\vec{x}_{j}$ are linearly independent.

Which of the following statements regarding the graph $G$ must be TRUE, for any such vectors $\vec{x}_{1}, \vec{x}_{2}, \ldots, \vec{x}_{m}$ ? Recall that a clique in a graph is a set of vertices $S \subseteq V$ that have an edge between every pair of vertices in $S$.

• A. If $m>d$, the graph must be disconnected.
• B. Any clique has size at most $d$
• C. Any clique has size at most $m / 2$
• D. The maximum degree of any vertex in $G$ is at most $d$
• E. None of the above.

   

Answer 1

Lets consider the vectors in $\mathbb{R}^3{}$ space   =

                                           Set  S     =      $\begin{cases} &\begin{bmatrix}a \\ b \\ c \end{bmatrix} \left.\begin{matrix} \\ \\ \end{matrix}\right|             \forall a,b,c \in \mathbb{R} \end{cases} \left.\begin{matrix} \\ \\ \\ \end{matrix}\right\}$ 

                                                       i.e,          $\begin{cases} & \begin{bmatrix}1 \\ 0 \\ 0 \end{bmatrix} \end{cases}$$,\begin{bmatrix}0 \\ 1 \\ 0 \end{bmatrix}$,$\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$,$\begin{bmatrix} 1 \\ 0 \\ 1 \end{bmatrix}$,$\begin{bmatrix} 2 \\ 5 \\ 1 \end{bmatrix}$,………...$\left.\begin{matrix} \\ \\ \\ \end{matrix}\right\}$

Lets disprove the options one by one…

                                  A pair of vectors  $\vec{x}$  and $\vec{y}$ are linearly independent if and only if one vector cannot be represented as scalar multiple of other vector

                                           i.e,   $\begin{cases} &\begin{bmatrix}a \\ b \\ c \end{bmatrix},\begin{bmatrix}x \\ y \\ z \end{bmatrix} \left.\begin{matrix} \\ \\ \end{matrix}\right|                \forall i \in \mathbb{R} \end{cases},   i*\begin{bmatrix}a \\ b \\ c \end{bmatrix} $$\neq$$ \begin{bmatrix}x\\ y \\ z \end{bmatrix} \left.\begin{matrix} \\ \\ \\ \end{matrix}\right\}$ 

For eg : $\left\{\begin{matrix} \\ \\ \\ \end{matrix}\right.\begin{bmatrix}1\\ 0\\ 0\end{bmatrix} ,\begin{bmatrix}0 \\ 1 \\ 0 \end{bmatrix} \left.\begin{matrix} \\ \\ \\ \end{matrix}\right\}$ is a pair of linear independent vectors

Conider the below graph

                            

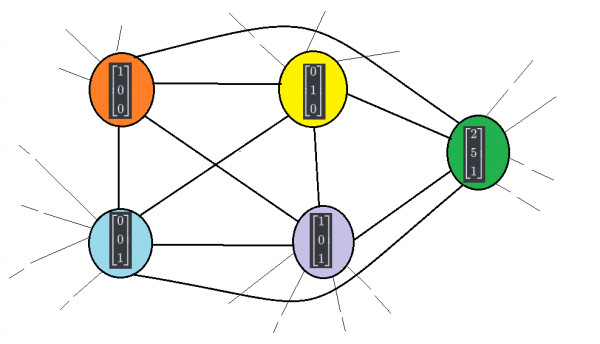
Here we can see that the size of the clique is 5  where d = 3 ,we can eliminate Option B right away…

Option C can be disproven by considering a set of 6 vectors (m=6) taking above five vectors in the set along with any other vector

{ m/2 = 3 but the size of the clique is 5 }

The maximum degree of a vertex can be anything hence Option D can be eliminated

For every vector in set ,there exist  atleast one corresponding linear independent vector to which it makes

up an edge in the graph . Hence Option A is eliminated as no vertex can be idle without an edge incident on it…

Hence Option E is the answer…...