Models of Computation - Find an NFA with two states that accepts the following language

Question

Find an NFA with two states that accepts the following language:

L = {aⁿ : n ≥ 1} ∪ {b^ma^k : m ≥ 0, k ≥ 0}.

Comments

two states q0 and q1 with transition

{q0, b} = q0

{q0, a} = q1

{q1, a} = q1.

Answer 1

$\{a^n : n \geq 1\}$ is a subset of $\{b^ma^k : m \geq 0, k \geq 0\}$.

So, their union will be : $\{b^ma^k : m \geq 0, k \geq 0\}$

Since, the question is asking for an NFA, we do not need to draw all transitions. So, here it is:

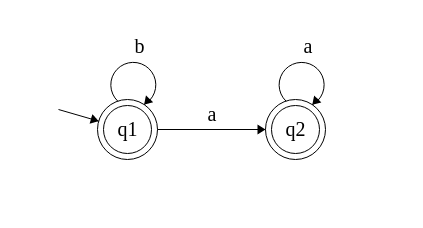
The missing links lead to a dead state.