Answer $509$
For 1000 elements, there will be 10 levels (root is at level 1). But last level will not be completely filled since there are only 1000 elements.
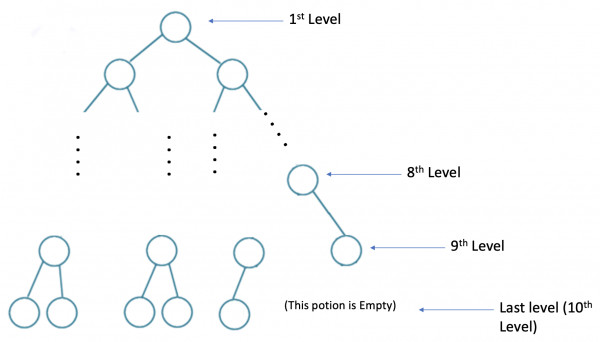
As you can see, some portion is empty. Since largest element can not have children as there are not enough nodes. – we need 1023 nodes to fill all levels.
Now lets see if $A$ in below diagram has children ?
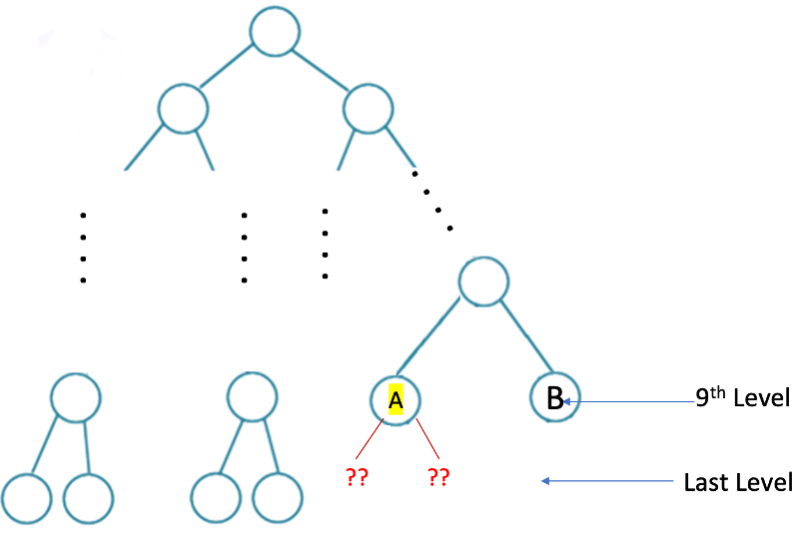
Again, we do not have enough nodes that’s why A will not be having subtree. (This is key point in this question, let’s have a quick explanation of why A doesn't have any children.)
Total nodes till 2nd last level = $2^9-1 = 511$
If we want to fill the last level completely, we need = $2^{10}-1 = 1023$ nodes.
A and B can have just 2 children each, so for 1023-4 = 1019 nodes, A and B does not have children.
for 1020 nodes, A has a left child
for 1021 nodes, A has both children, for 1022 nodes, B has a left child, and for 1023 nodes, B has both children.
Now,
largest will be at rightmost of 9th level, (Easy to see…..just keep going right)
2nd largest will at rightmost of 8th level, (because if you want to find larger than this then you need to go on right side and there is just one element on right side)
Where will be $3^{rd}$ largest ?
Since we know that inorder of BST is sorted hence 3rd largest will be a element just before 2nd largest in inorder. What we call such element ? – inorder predecessor.
Hence 3rd largest will be inorder predecessor of 2nd largest. – which is $A$ in above diagram.
Lets find index of 2nd largest then we can find index of 3rd largest.
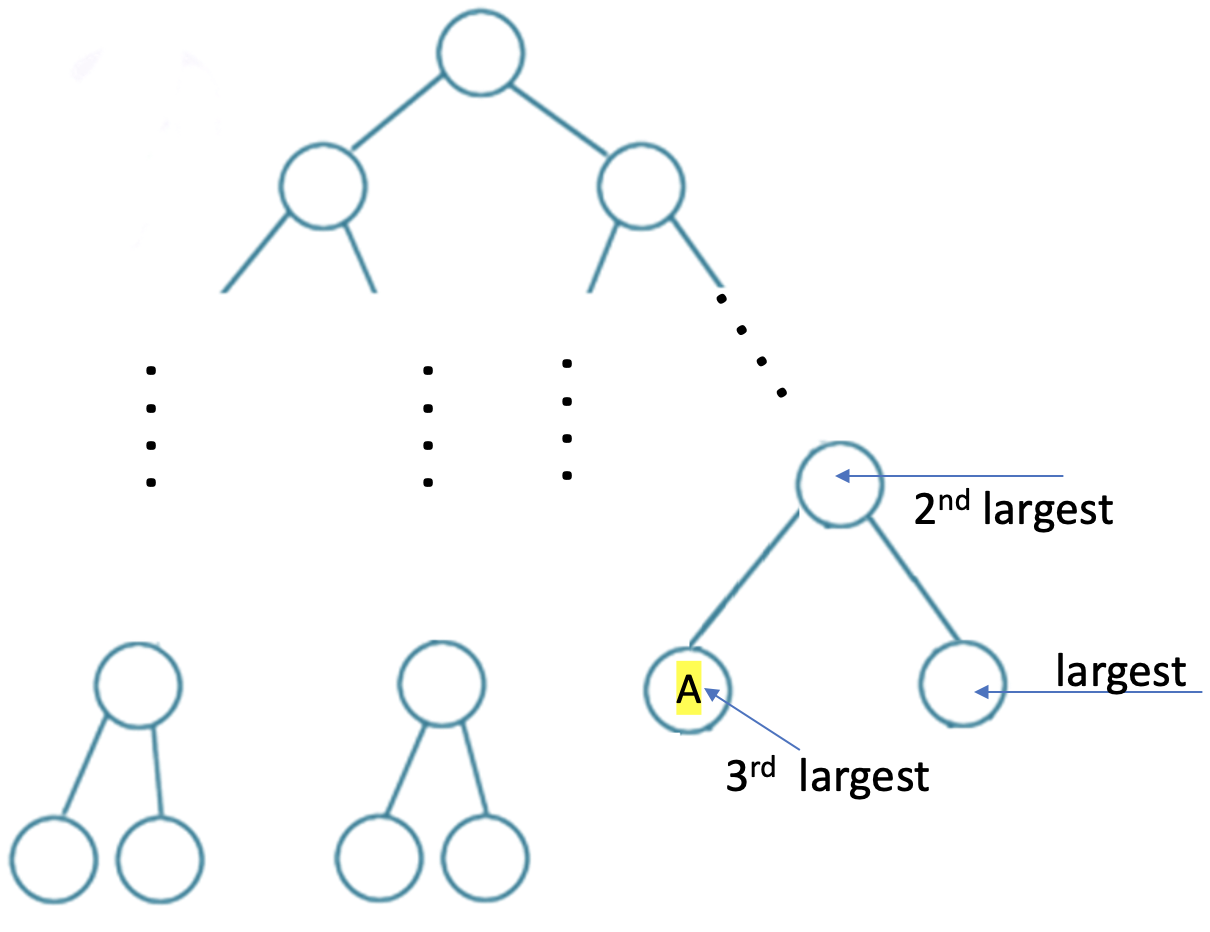
index of 2nd largest. (Assuming index starts from 1)
$1 \rightarrow 3 \rightarrow 7 \rightarrow 15 \rightarrow 31 \rightarrow 63 \rightarrow 127 \rightarrow 255$
Index of 3rd largest = $510$
Since indices are starting from 0 hence answer is $509$