GATE CSE 2024 | Set 1 | Question: 17

Question

Let $A$ and $B$ be two events in a probability space with $P(A)=0.3, P(B)=0.5$, and $P(A \cap B)=0.1$. Which of the following statements is/are TRUE?

• A. The two events $A$ and $B$ are independent
• B. $P(A \cup B)=0.7$
• C. $P\left(A \cap B^c\right)=0.2$, where $B^c$ is the complement of the event $B$ 
• D. $P\left(A^c \cap B^c\right)=0.4$, where $A^c$ and $B^c$ are the complements of the events $A$ and $B$, respectively 

Answer 1

The fastest way to solve these type of question is with the help of Venn Diagram. 

For this question, Venn Diagram will look like this : 

 

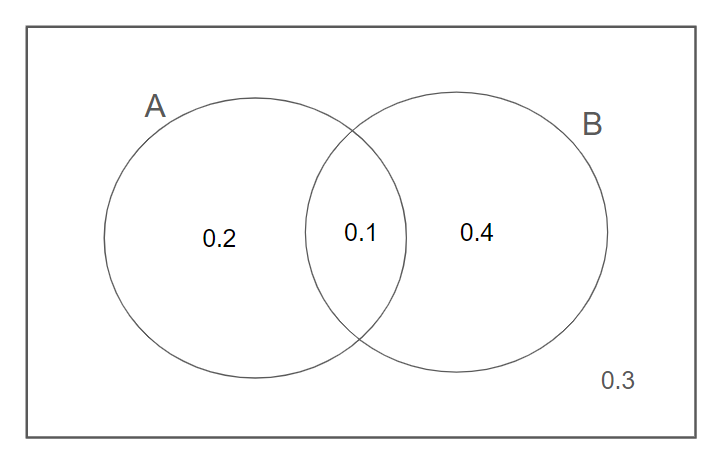
P(A) = 0.3, P(B) = 0.5, P(A  $\cap$ B) = 0.1

Let's try to observe every option one by one.

 

Option A : The two events 𝐴 and 𝐵 are independent

Two events are said to be Independent when : P(A $\cap$ B) = P(A).P(B)

P(A $\cap$ B) = 0.1

P(A).P(B) = 0.3 x 0.5 = 0.15

P(A $\cap$ B) $\neq$ P(A).P(B)

So, Option A is Incorrect.

 

Option B : P(A $\cup$ B) = 0.7.

P(A $\cup$ B) = P(A) + P(B) - P(A $\cap$ B) 

= 0.3 + 0.5 - 0.1 = 0.7

So, Option B is Correct.

 

Option C : P($A \cap B^{c}$) = 0.2

P($A \cap B^{c}$) = P(A-B) = P(Only A) = 0.2

From Above Venn diagram it is clear that this is True.

So, Option C is Correct.

 

Option D : P($A^{c} \cap B^{c}$) = 0.4

P($A^{c} \cap B^{c}$) = P($(A \cup B)^{c}$) = 1 - P(A $\cup$ B)

From venn diagram it is clear that this value is 0.3 not 0.4.

This statement is False.

So, Option D is Incorrect.

 

---

 

Correct Answer : B, C

Answer 2

P(A u B) = 0.7, Option B is correct

P(A)*P(B) = 0.15, Option A is incorrect as for independent events P(A n B) = P(A)*P(B)

For C, it will be equal to P(A) - P(A n B) = 0.3 - 0.1 = 0.2, So C is correct

For D, it is 1 - P(AuB) = 1 - 0.7 = 0.3, So D is incorrect.

Answers: B,C