A push down automation (pda) is given in the following extended notation of finite state diagram:
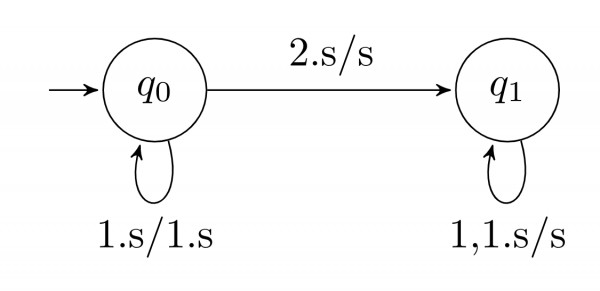
The nodes denote the states while the edges denote the moves of the pda. The edge labels are of the form $d$, $s/s'$ where $d$ is the input symbol read and $s, s'$ are the stack contents before and after the move. For example the edge labeled $1, s/1.s$ denotes the move from state $q_0$ to $q_0$ in which the input symbol $1$ is read and pushed to the stack.
- Introduce two edges with appropriate labels in the above diagram so that the resulting pda accepts the language $\left\{x2x^{R} \mid x \in \left\{0,1\right\}^*,x^{R} \text{ denotes reverse of x}\right\}$, by empty stack.
- Describe a non-deterministic pda with three states in the above notation that accept the language $\left\{0^{n}1^{m} \mid n \leq m \leq 2n\right\}$ by empty stack