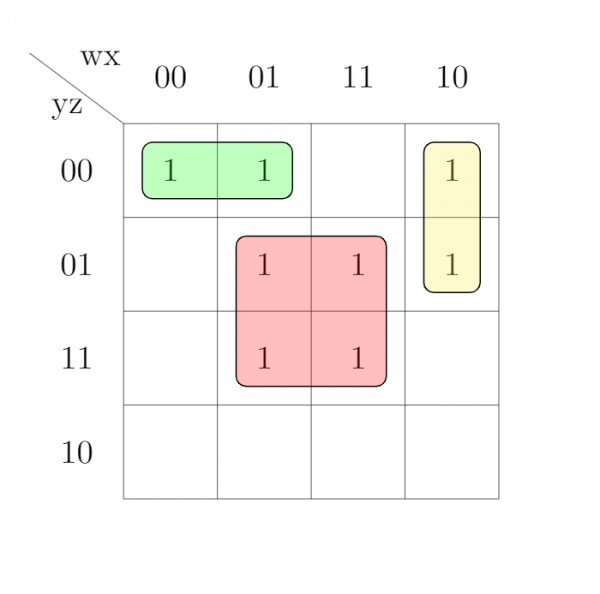
 K-map
K-map
So, minimized expression will be
$xz + w'y'z' + wx'y'$ which is Q. From the K-map, we can also get P and R. So, only S is NOT equivalent to $f$.
http://www.eecs.berkeley.edu/~newton/Classes/CS150sp98/lectures/week4_2/sld011.htm
Alternatively,
Go with Minterm representation of each option, (Note that order of $W,X,Y,Z$ should be preserved.)
Here, $x$ means do not care ($x$ takes value either $0$ or $1$)
$P : X' Y' Z' + W' X Y' + W Y' Z + X Z$
$\qquad = x X' Y' Z' + W' X Y' x + W x Y' Z + x X x Z$
$\qquad= x 000 + 010x + 1 x 01 + x 1 x 1$
$\qquad= 0000 + 1000 + 0100 + 0101 + 1001 + 1101 + 0101+0111+1101+1111$
$\qquad= 0 + 8 + 4 + 5 + 9+13 + 5+7+13+15$
$\qquad= ∑ m(0,4,5,7,8,9,13,15)$
$Q : W' Y' Z' + W X' Y' + XZ$
$\qquad= W' x Y' Z' + W X' Y' x + x X x Z$
$\qquad= 0 x 0 0 + 100 x + x 1 x 1$
$\qquad= 0000+0100 + 1000+1001 + 0101 + 0111+1101+1111$
$\qquad= 0+4 + 8+9 + 5+7+13+15$
$\qquad= ∑ m(0,4,5,7,8,9,13,15)$
$R : W' Y' Z' + W X' Y' + XYZ + X Y' Z$
$\qquad= W' x Y' Z' + W X' Y' x + x X Y Z + x X Y' Z$
$\qquad= 0 x 0 0 + 100 x + x 111 + x 101$
$\qquad= 0000+ 0100 + 1000+1001 + 0111+1111 + 0101 + 1101$
$\qquad= 0+4 + 8+9 + 7+15 + 5+13$
$\qquad= ∑ m(0,4,5,7,8,9,13,15)$
$S : X' Y' Z' + W X' Y' + W' Y$
$\qquad= x X' Y' Z' + W X' Y' x + W' x Y x$
$\qquad= x 000 + 100 x + 0 x 1 x$
$\qquad= 0000+1000 + 1000+1001 + 0010+0011+0110+0111$
$\qquad= 0+8 + 8+9 + 2+3+6+7$
$\qquad= ∑ m(0,2,3,6,7,8,9)$
Correct Answer: $D$