Extending the comment by @Vineet Kumar 1
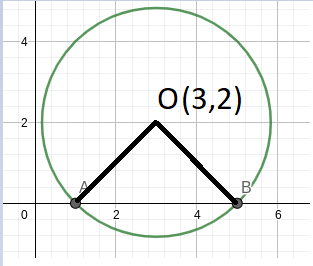
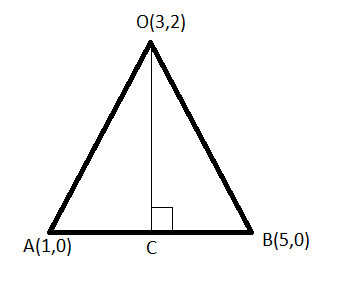
$OC$ is perpendicular on $AB$ and divides it in two equal parts
Let $\angle OAB = \theta$,
$cos\theta = \frac{OC}{OA} = \frac{2}{2\sqrt{2}}=\frac{1}{\sqrt{2}}$
$\theta = 45$
So, In $\triangle OAB,\angle OAB + \angle OBA + \angle AOB = 180$
Also, $\angle OAB = \angle OBA$. So, $\angle AOB=90$
So, Area of the required part $=$ Area of Sector $OAB$ $- $Area of triangle $OAB$
$= \pi r^2 * \frac{\angle AOB}{360}\,\,-\,\,\frac{1}{2}*OC*AB$
$= \pi (2\sqrt{2})^2 * \frac{90}{360} \,\,-\,\, \frac{1}{2}*2*4$
$=2.28$
Correct me if I'm wrong