I am using two AND gates and a NOT gate along with 3 flip flops.
there are 6 unique states. lets assume there is a synchronous counter the generates below sequence:
100->001->101->010->110->011->100.
Let output of 3 flip flops be S1, S2 , S3. Take them through below circuit 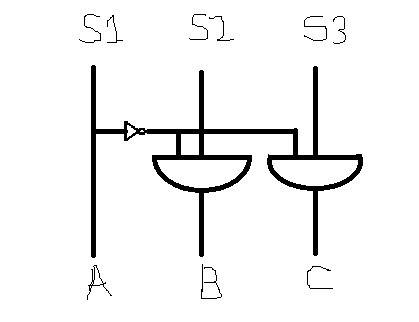
| S1 |
S2 |
S3 |
A |
B |
C |
|---|
| 1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
0 |
0 |
| 0 |
1 |
0 |
0 |
1 |
0 |
| 1 |
1 |
0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
1 |
1 |
if we take B C as final output we can generate 0->1->0->2->0->3.
So I think it is possible with 3 flip flops.
Requesting comments.