The Given inputs I1(0), I2(1), I3(R), I4(R)
and Selection line S0(P) and S1(Q)
Hence final Output F= (S0)'.(S1)'.I1 + (S0)'.(S1).I2 +(S0).(S1)'.I3+(S0).(S1).I4
F= P'.Q'.I1 + P'.Q.I2 +P.Q'.I3 +P.Q.I4
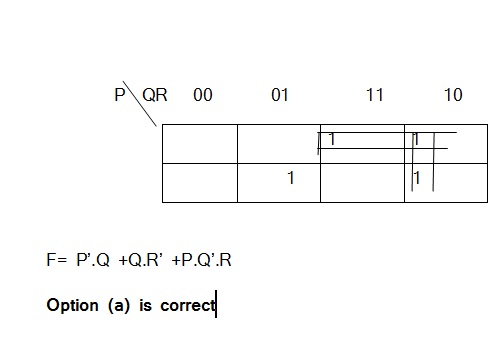
F=P'.Q'.0 + P'.Q.1+P.Q'.R +P.Q.R'
F= P'.Q.+P.Q'.R +P.Q.R' but this equation does not match any option so we draw K-Map