why is the conclusion incorrect for the below premises ?

Question

 

I am getting the conclusion to be true by Proof by Contradiction , what's wrong in the approach ?

Answer 1

$\text{No plane is hill}$              $\forall x \left ( plane(x) \rightarrow \sim hill(x) \right )$ ...............................1

$\text{Some hills are towns}$    $\exists x (hill(x) \wedge town(x) )$ ...................................2

 

Conclusion : 

$\text{No town is plane    }$ $\forall x (town(x) \rightarrow \sim plane(x))$ ....................... 3

Assuming "No town is plane" is false 

So, $ \sim \forall x (town(x) \rightarrow \sim plane(x))$

$\exists x \sim (town(x) \rightarrow \sim plane(x))$

$\exists x \sim (\sim town(x) \vee \sim plane(x))$

$ \exists x  ( town(x) \wedge plane(x)) $ ...................... 4

Now 3 and 4 can both be true because premises 1 and 2 are not sufficient to conclude 3.

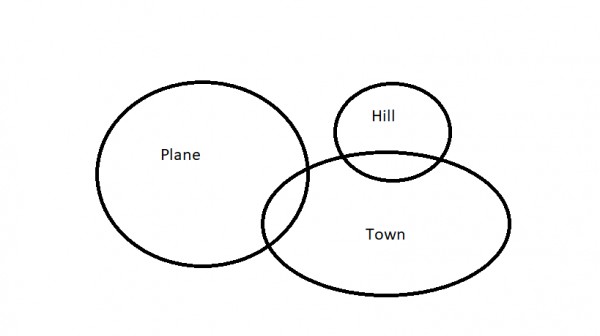
The scenario above is true for both the premises and also true for 4. There exists a town which is plane.

 

The scenario above is true for both the premises and also true for 3. No town is plane.

So premise 1 and 2 are not sufficient enough to conclude $\text{No town is plane}$

Comments

hill(x) must be true but we substituted it to be false in premise 1

Look 1st can only be true when there is no intersection between P and H

$\forall x \sim  (P(x) \wedge H(x))$ what this means is "it is not possible for any so be true for both P(x) and H(x).

$\exists x (H(x) \wedge T(x))$ what this means " there exists x which is true for both H(x) abd T(x)"

Now when you say substituting H(x) as false and P(x) as true in 1st premise, you're saying for all x H(x) is false and P(x) is true.

Ok assuming this we move on to next premise which is $\exists x (H(x) \wedge T(x))$ now this becomes false so we substituted wrong values in 1st premise as there exist x which is H(x).

now if we take P(x) false for all x and H(x) true for all x we are saying that there doesn't exists any Plane and everything is H and there exists x which is both H and T. from this we conclude no town is plane as there doesn't exist any plane in the first place.

But where we go wrong?

$\forall x \sim  (P(x) \wedge H(x))$ here.

As we cannot substitute H(x) false  for all x

that statement means there exists no x for which both P(x) and H(x) if true and doesn't mean either all x are P(x) or all x are H(x).

$\forall x \sim  (P(x) \wedge H(x))$ or $\sim \exists  x  (P(x) \wedge H(x))$

can be true in 3 conditions 

1. there exists x which P(x) but not H(x)
2. there exists x which H(x) but not P(x)
3. there exists x which is not H(x) neither P(x)

3rd condition is true when 

some x are town but are not plane and also not hill.

The problem with your proof is you are substituting values and not caring about the values that can be substituted and can conclude opposite of $\sim (T(x) \wedge P(x))$

 

---

Thanks a lot for bearing with me , I understood now .

---

radha gogia no problem i hope you got my point and if not feel free to comment