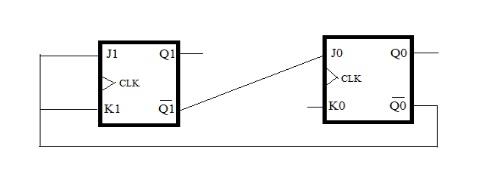
 Assume the initial values of $K0$, $Q_0$ and $Q_1$ to be $1$.
Assume the initial values of $K0$, $Q_0$ and $Q_1$ to be $1$.
Which of the following state transition tables correctly correspond to the circuit given above? (Note: $Q_{kN}$ and $Q_{kN+1}$ represent current and next state respctively)
- $\begin{array}{|c|c|c|c|} \hline Q_{1N} & Q_{0N} & Q_{1N+1} & Q_{0N+1} \\ \hline 1 & 1 & 1 & 0 \\ \hline 1 & 0 & 0 & 0 \\ \hline 0 & 0 & 1 & 1 \\ \hline \end{array}$
- $\begin{array}{|c|c|c|c|} \hline Q_{1N} & Q_{0N} & Q_{1N+1} & Q_{0N+1} \\ \hline 1 & 1 & 0 & 1 \\ \hline 0 & 1 & 0 & 0 \\ \hline 0 & 0 & 1 & 1 \\ \hline \end{array}$
- $\begin{array}{|c|c|c|c|} \hline Q_{1N} & Q_{0N} & Q_{1N+1} & Q_{0N+1} \\ \hline 1 & 1 & 1 & 0 \\ \hline 1 & 0 & 0 & 1 \\ \hline 0 & 1 & 1 & 1 \\ \hline \end{array}$
- $\begin{array}{|c|c|c|c|} \hline Q_{1N} & Q_{0N} & Q_{1N+1} & Q_{0N+1} \\ \hline 1 & 1 & 0 & 0 \\ \hline 0 & 0 & 0 & 1 \\ \hline 0 & 1 & 1 & 1 \\ \hline \end{array}$