This property (B) is a well known property from integration… Please add it to the correct options
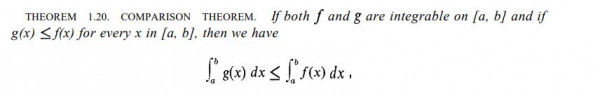
Source: Tom M. Apostol – Calculus Vol-1 2nd Edition
Note:
Saying, f and g are continuous for all $x \epsilon [a,b]$ is equivalent of saying both f and g are integrabele on [a,b]