"With $2^n:1$ Mux, We can implement all n variable functions, and some n+1 variable function"
Lets take a small example, with n=3:
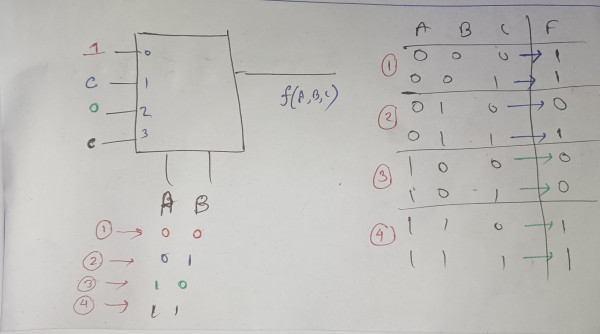
f(A,B,C) = Σm(0, 1, 3, 6, 7)
A B C F
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
We can easily implement this with $2^3 * 1$ Mux
The implementation is:
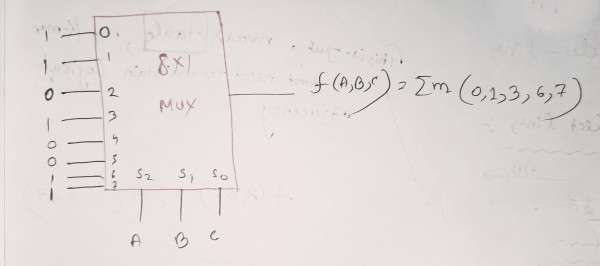
Now Lets take another function, f (A,B,C) = Σm(2, 4, 5, 6)
Can we implement this 3 var function with $2^2 \times 1$ i.e $4 \times 1$ Mux ?
No, as 4 x1 Mux have only 4 inputs but we have total 8 inputs.
So, Not possible.
But if we have an extra NOT gate, then we can implement this easily.
A B C F
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 0
Now check the below implementation:
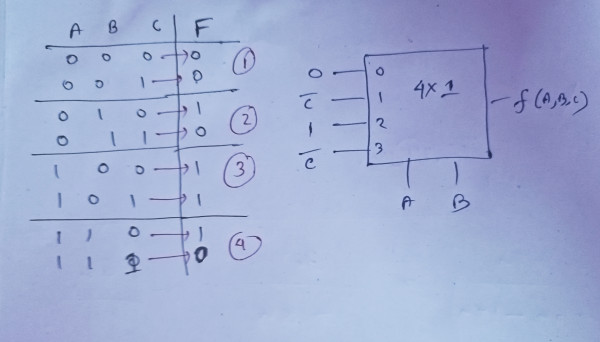
Here, we have taken A, B as Select lines, so it will have 00, 01, 10, and 11 combinations and the output will depend on C inputs.
Now if we observe the truth table, we will find F values in 1st and 3rd case are independent of C.
But in 2nd and 4th case it is complement of C.
That why here we need a Not gate to take complement of C as Input.
So we can implement this 3 var function with 2³⁻¹ MUX using an extra NOT gate.
In general,
If Invertor is available, then we can implement n var function with 2ⁿ⁻¹ x 1 MUX
So Option C. is the correct ans.
Note:
We can use $2^n \times 1$ Mux to implement “some” $n+1$ var functions also “without Using NOT gate”
f(A,B,C) = Σm(0, 1, 3, 6, 7)
A B C F
0 0 0 1
0 0 1 1
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 1
1 1 1 1
We can implement this using 4x1 Mux without using any NOT gate also (even though it is 3 var fun)