GATE CSE 2013 | Question: 26

Question

The line graph $L(G)$ of a simple graph $G$ is defined as follows:

• There is exactly one vertex $v(e)$ in $L(G)$ for each edge $e$ in $G$.
• For any two edges $e$ and $e'$ in $G$, $L(G)$ has an edge between $v(e)$ and $v(e')$, if and only if $e$ and $e'$ are incident with the same vertex in $G$.

Which of the following statements is/are TRUE?

• (P) The line graph of a cycle is a cycle.
• (Q) The line graph of a clique is a clique.
• (R) The line graph of a planar graph is planar.
• (S) The line graph of a tree is a tree.
   

• A. $P$ only
• B. $P$ and $R$ only
• C. $R$ only
• D. $P, Q$ and $S$ only

Comments

Got it...thanks

---

Take original graph as star graph. Line graph will be complete graph. That would eliminate option $R$ and $S$.

Take $K_4$ to eliminate option $Q$

---

I considered cycle and planar graphs and used reverse engineering to derive the results for options S and R

 

Answer 1

P) True. Because every edge in cycle graph will become a vertex in new graph $L(G)$ and every vertex of cycle graph will become an edge in new graph.

R) False. We can give counter example. Let $G$ has $5$ vertices and $9$ edges which is a planar graph. Assume degree of one vertex is $2$ and of all others are $4$. Now,  $L(G)$ has $9$ vertices (because $G$ has $9$ edges ) and $25$ edges. (See below). But for a graph to be planar $|E| <= 3|V| - 6$.

For $9$ vertices $|E| \leq 3*9 - 6$

$⇒|E| \leq 27 - 6$

$⇒|E| \leq 21$. But $L(G)$ has $25$ edges and so is not planar.

As R) is False option (B), (C) are eliminated.
http://www.personal.kent.edu/~rmuhamma/GraphTheory/MyGraphTheory/planarity.htm

S) False. By counter example. Try drawing a simple tree which has a Root node ,Root node has one child A, node A has two child B and C. Draw its Line graph acc. to given rules in question you will get a cycle graph of $3$ vertices.

So (D) also not correct.

$\therefore$  option (A) is correct.

---

For a graph G with n vertices and m edges, the number of vertices of the line graph L(G) is m, and the number of edges of L(G) is half the sum of the squares of the degrees of the vertices in G, minus m.

Comments

@halfcodeblood, Counter example is already available in the comments, rt ?

---

nice explaination

---

Q) The L(G) of a clique is clique. -  False

Let's Take a Clique G.

K₄

n = 4, e = 6

In its L(G) ,

n = 6, e = 3 + 3 + 3 + 3 = 12 (See Sachin Sir's Comment, He gave a formula to count the no. of edges in a Line graph)

So, for L(G) to become a clique, it needs 15 edges, but it has only 12.

Hence, The statement is FALSE

Answer 2

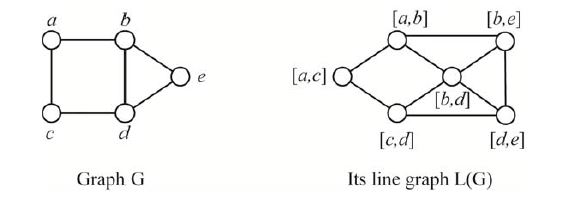
L(G) is a 2-set {e1,e2} of edges in G with which are adjacent to a common vertex v. This vertex v is uniquely determined by {e1,e2}. 

If a vertex vv has degree d, there are (d2) 2-sets{e1,e2} such that e1 and e2 are adjacent to v

So the total number of edges in L(G) is 

$\sum_{i=0}^{n}\binom{n}{2}=n(n-1)/2$

There is very simple and easy proof to drive expression for number of edges in lines graph- 

Comments

perfect saket :)

---

@Saket, Sir how u have found number of edges in line graph? Which formula u r using?

---

Just small correction

Formula for finding no of edges in L(G):

If a vertex v has degree d, there are C(d,2) 2-sets {e1,e2} such that e1 and e2 are adjacent to v
So the total number of edges in L(G) is 

From i=1 to n ,∑C(d_i,2) =∑d_i(d_i−1) / 2 ,where i is vertex and d_i is degree of vertex i and n is the total no vertices in G.

---

last calculation is having some mistake,

no. of edges = $\frac{4*3}{2} + \frac{3*2}{2} + \frac{4*3}{2} + \frac{3*2}{2} + \frac{4*3}{2}$ =  6 + 3 +6 +3 +6 =24

Answer 3

Answer is  option (A)

Comments

underrated answer .

---

Although the answer is correct, the solution is not. Line graph of K4 is planar 

https://math.stackexchange.com/questions/3018581/is-lk4-graph-planar

---

Great explanation

Answer 4

Everything you need to know about LINE GRAPHS

 

You won’t find anything better than this anywhere as its from NPTEL IIT MADRAS.

 

Comments

Please give the link to the source.

Answer 5

i think

(A) P only

because by taking a simple graph of 4 vertices(i.e planar graph)(take a 2 regular graph) and we can some to know it's planar    :    option C eliminated ,

but tree for tree is not possible as it seems to be a cycle : option D eliminated.

also planar doesn't seem possible ,

hence possible answer is option A.

Comments

Oh u mean two vertex is coincide in the same point (ab coincide in a...) . R u sure it happens for any grah?

Planar graph are those graph in which no edge can intersect other. So how planar concept can be eliminated?

---

take any complex example and you will see that the graph becomes non-planar,in my photo take an edge from a to c(diagonal) and you will see G2 becoming non-planar.

also, in any case cycle in G1 has to give cycle in G2.

---

Yes. Taking examples is the better way to do, unless you know more about line graphs. 

http://mathworld.wolfram.com/LineGraph.html

Answer 6

https://www.youtube.com/watch?v=B6bn7ovzNBM

Must watch