GATE CSE 1989 | Question: 3-vi

Question

Which of the following graphs is/are planar?

Comments

only G2 is planer

---

If sub-graph of any given graph is $K_{5}$ or $K_{3,3}$  then that graph is non planner graph. Because $K_{5}$ and $K_{3,3}$ are smallest non planner graph in terms of number vertices and number edges respectively.

---

Thanks

---

https://www.youtube.com/watch?v=wnYtITkWAYA

 

this might help

Answer 1

$G_1$ is $K_{3,3}$ which is a non-planar graph with the minimum number of edges.

Proof: Let $K_{3,3}$ is a planar graph.
Therefore it must satisfy this useful corollary. As there is no triangle in  $K_{3,3}$.

• Let $G$ be a connected planar simple graph with $n$ vertices and $m$ edges, and no triangles. Then $m \leq 2n - 4$

$m = 9, n = 6.$
$\implies 9 \leq12 - 4$
$\implies 9 \leq8,$ which is false. So our assumption that  $K_{3,3}$ is planar is false.

$G_2$ can be redrawn like this.

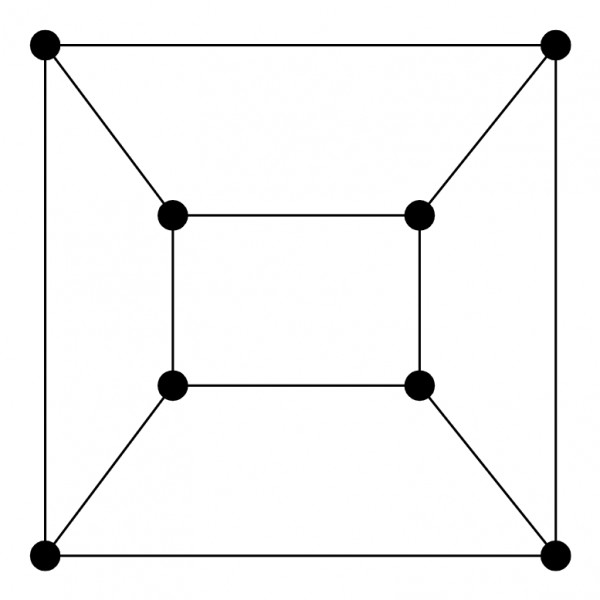
Therefore $G_2$ is a planar graph.

For $G_3$, we assume that it is a planar graph. Then it must satisfy the above corollary as it does not have a triangle.

$m = 9, n = 6.$
$\implies 9 \leq 12 - 4$

$\implies 9 \leq 8,$ which is false. So our assumption is wrong and $G_3$ is not a planar graph.

Note$: G_1$ and $G_3$ are isomorphic graphs. 

Ans: $G_2$ only.

Comments

@chhotu it is correct. You can verify it here. :) 

http://www.personal.kent.edu/~rmuhamma/GraphTheory/MyGraphTheory/planarity.htm

---

Yes ,Graphs G1 and G3 both are K_3,3 Kuratowski 2nd graph which is a Non-planar graph.

---

@Hemant Parihar 

Given a simple planar graph we can say using Euler theorem:

1.  $edges \leqslant 3n-6$

2.$faces \leqslant 2n-4$

How you used 2n-4 for edges? :(

---

Sorry I missed "no triangles" . This is one more corollary. Thanks for the link :)

---

actually  i) and iii) are the same graphs and they are K(3,3). Therefore, both are not planar.

Answer 2

graph G2 is planar because we can draw all its edges without crossing each other .

Comments

Please give me some reference material link from where i can study further about graph.

---

refer kenneth rosen

---

thanks...!

Answer 3

you can remember this points to solve this type of questions:

1. Km,n is planar iff m<=2 or n<=2
2. Q3 is planar as it has isomorphic structure G2 as shown in BEST answer below 
3. G3 shown here is isomorphic with K 3,3 

Answer 4

Only G2 is planar. Verify it by making diagrams.